高速磁浮车辆弹性悬浮架动力学建模与仿真

    
    2．2模态分析
   
    将建立的悬浮架超单元调入ANSYS中进行模态分析，为了保持sIMPACK与ANSYS环境中悬浮架的刚体自由度一致，不对其施加任何约束。表2列出了悬浮架的模态自振频率，图3显示了悬浮架的前网阶模态振型。表2说明悬浮架前四阶频率分别为6．40Hz、7．61Hz、11．39Hz和21．24Hz，图3表明其对应的模态振型分别为纵向扭转、横向弯曲、竖向弯曲以及纵向扭转+横向弯曲。可见，悬浮架的结构自振频率低、振型丰富；扭转频率最低，表明其抵抗扭转变形的能力较差。因此，开展磁浮车辆动力学分析特别是曲线通过仿真时，有必要考虑悬浮架的弹性变形。
   

    3高速磁浮车辆刚弹性动力学模型
   
    利用SIMPACK软件，建立磁浮车辆除悬浮架之外的其它部件如车体、摇枕、摆杆、牵引拉杆、导向磁铁、悬浮磁铁等的刚体模型。同时，将弹性悬浮架有限元分析的结果文件调入FEMBS模块，经过数据转换得到．SID FEM文件和CAD文件，然后在SIMPACK中调用该文件，从而建立弹性悬浮架模型。进一步建立各部件(包括弹性悬浮架)之间的连接关系(弹簧、阻尼等力与约束关系，以及电磁悬浮与导向控制系统模型等，最终得到如图4所示的高速磁浮车辆刚弹性动力学分析模型。其中．电磁悬浮和导向系统均采用了基于状态估计的反馈控制。
   

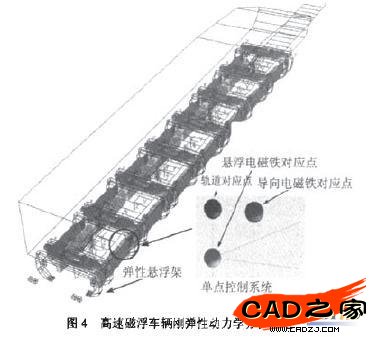
    4弹性悬浮架通过曲线时的动态响应
   
    4．1曲线线路条件
   
    以上海高速磁浮线上半径最小的平面曲线作为仿真计算的线路条件，参数如下：圆曲线半径Rc=2260m，圆曲线长度Rc=250m，圆曲线横坡角θc=12°，轨距S=2．22m，缓和曲线长度lt=500m。
   
    上海磁浮线平面曲线采用了正弦线形缓和曲线，线路的中心高程不变，缓和曲线段线路表面是一个空间扭转曲面。正弦线形缓和曲线的曲率、横坡角及其导数公式:
   

    SIMPACK Track菜单没有正弦线形缓和曲线选项，实际建模时需编制曲线线路数据文件，采用SIMPACK轨道文件制作程序生成．unf文件，然后在Track菜单调用该文件，即可建立曲线轨道模型。
   
    4．2仿真结果分析
   
    为了更好地分析弹性悬浮架曲线通过的响应规律，仿真计算时不考虑轨道几何不平顺激扰的影响，车辆速度取曲线平衡通过速度250km/h。结果分析中悬浮架上某点的弹性变形量均指该点相对于悬浮架质心的位移量。
   
    图5是第四(尾部)悬浮架上8个弓形脚铰点的垂向弹性变形曲线。由图5可见，第2、4位和第5、7位铰点的弹性变形较大，最大变形量为一2．51mm(负号表示方向向上)，同一时刻上述四个铰点的变形方向相同，但各点的变形方向在前、后缓平u曲线段刚好相反。第1、3位和第6、8位铰点的弹性变形相对较小，小于0．8mm，变形方向分别与其对应的第2、4位和第5、7位相反。
   

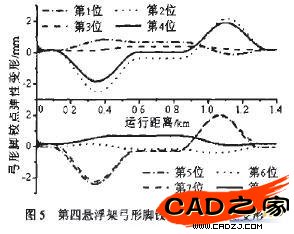
    图5中弓形脚铰点的弹性变形量包括了悬浮架整体扭转引起的位移最和悬浮臂局部的弹性变形量。为了区分这两种弹性变形，计算了弓形脚铰点相对于横粱上垂直对应点的位移量，即悬浮臂的弹性变形量。图6给出了悬浮臂弹性变形量随运行距离的变化曲线，它表明悬浮臂变形主要发牛在前后缓和曲线段，最大弹性变化量为0．44mm，是整体弹性变形最大值的17．6％。可见，弓形脚铰点的弹性位移主要来源于悬浮架的扭转变形。