基于UG在计算几何图形的长度、面积中的应用

　　1引言

　　CAD、CAM、CAE软件发展到现在，已经形成了众多模块，功能越来越多，越来越强大。运用软件提供的功能，我们能够更快、更好和更准确的解决问题。计算机的诞生，就是为了把人们从繁重的劳动中解脱出来，而软件的出现则是为了更有效地使用计算机，所以充分运用软件的功能可以极大地减少我们今后工作中的计算量。

　　UG是集CAD/CAM/CAE一体的三维参数化软件，是当今世界最先进的计算机辅助设计、分析和制造软件，广泛应用于航空、航天、汽车、造船、通用机械和电子等工业领域。使用UG软件将使我们在工作中如虎添翼。本文通过使用UG软件计算几何图形的长度、面积这两个问题来证明使用软件的便利性，希望能够给大家一点启发。

　　2长度问题

　　已知三角形ABC(如图一)，AB长74，AC长45，BC长69，DE平行于BC，DE与BC之间的距离是20。当DE的长度为何值时，EC的长度会等于DE的长度。

　　我估计，大部分人拿到这个题目，都会马上找出纸和笔进行纸上作业，而不会通过UG软件来解决此问题。只要是有高中数学知识的人一般都能解决这个问题。从数学理论上解决这个问题有很多的方法，如三角函数法、解析几何法、向量几何法和复数法等等。有兴趣的人可以自己研究一下,我用的是三角函数的方法。

　　我由观察得知，BDEC这条折线投影到BC上就与BC重合。于是得到第一个方程：

　　由上面的方法可以看出，用数学理论方法求解这个问题是多么的复杂，而且计算量非常之大。我们身处计算机时代，纯计算的事情应该完全交给计算机处理。本着这种思想，我想到了借助UG软件来减少工作量。

　　首先我们新建一个文件，然后进入建模环境，之后进入草图功能。进入草图后，我们先画三角形ABC，然后定出三条边的尺寸，如图二。

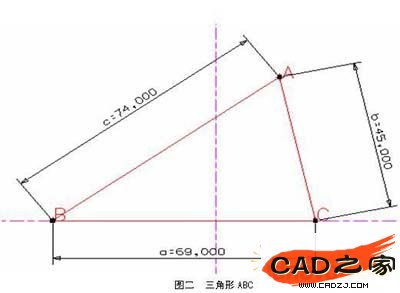
　　现在先随意画出DE和EC，然后我们用UG的约束功能约束DE平行BC，再给DE与BC之间定一个平行尺寸20，如图一所示。这样题目所给的已知量我们都画出来了,现在就剩下求出DE的长度了。

　　用过UG的人都知道UG草图中有约束功能，约束功能中有约束两条直线相等的选项。今天我们就是要使用这个选项。现在我们回到草图，约束DE与EC的长度相等，再用分析菜单中的距离功能量取DE的长度，这个长度即为我们所要求的长度。

　　有人要问：“怎么这么简单 ?”对，就是这么简单——因为所有的计算都是由UG软件完成的，你所做的只是移动与点击鼠标。这个方法说出来大家都会，可是真正在工作的时候会想起来的恐怕就没有几个人了。 UG软件从NX2升到NX5，功能日益强大。本文就UG在计算几何图形的长度、面积这两个问题上做一点介绍，希望能起到抛砖引玉的作用。

　　3三角形面积问题

　　已知等腰三角形ABC(如图三)，AB长70，AC长70，BC长100，DA长40，过D点做一线段DE交AC于E，使三角形ADE的面积为三角形ABC的一半，求此时DE的长度。 注：图三中p31这个尺寸不是已知条件，是我解决问题时设定的参数。

　　因为UG软件草图功能里没有约束面积相等这个选项，所以这个问题用刚刚的方法就行不通了。这里我将使用EXCEL电子表格进行设计优化的方法。

　　1)首先我们使用UG的BOUNDED PLANE 功能生成三角形ADE和四边形DECB，并给三角形ADE命名AREA1，给四边形DECB命名AREA2，如图四。这样问题就转化为求线段DE使三角形ADE和四边形DECB的面积相等。

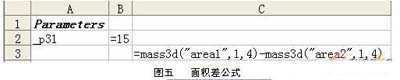
　　2)接下来我们从UG中打开EXCEL电子表格，在A1格提取表达式，删除不需要的尺寸，只留下_p31，即E点的Y坐标(参看图三)。然后在C3格输入：=mass3d("area1",1,4)- mass3d("area2",1,4)。 C3就是三角形ADE和四边形DECB的面积差,如图五所示。

　　3)接着我们就可以进行目标分析了，如图六所示。

　　目标分析的结果如图七所示：

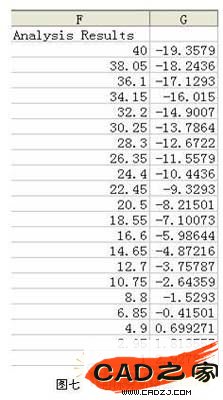
　　由图七可以看出当_p31这个尺寸在4.9到6.85之间变化时三角形ADE和四边形DECB的面积的差值由正转负，也就是说当_p31这个尺寸取4.9到6.85之间某个值时三角形ADE和四边形DECB的面积的差值为零，即三角形ADE和四边形DECB的面积相等。

　　4)这样我们锁定4.9到6.85这个区间进行目标搜索，如图八。

　　最后UG给我们的结果是当_p31等于6.123724的时候三角形ADE和四边形DECB的面积相等，它们分别等于1224.7448611928000000和1224.7448815904000000，从结果可以看出精确度非常之高。 UG软件从NX2升到NX5，功能日益强大。本文就UG在计算几何图形的长度、面积这两个问题上做一点介绍，希望能起到抛砖引玉的作用。

　　4曲边四边形面积问题

　　前面解决了一个三角形面积问题，现在我们做个曲边四边形面积问题，如图九所示。

　　已知曲边四边形ABCD，F为AB上一固定点，E为CD上一游动点，求E在CD上哪一点处曲边四边形AFED和曲边四边形EFBC的面积相等。(注：具体的尺寸省略，这里只讲方法)

　　这个问题不能使用电子表格进行目标分析和目标搜索。原因在于E点从D向C移动的过程中，EF的长度不是单调变化的。要求解这个问题，需要借助UG的二次开发功能。

　　1)首先，我们要在曲边CD上做出若干点，比如100个点，这要配合精度要求来取，精度越高，点数越多。

　　2)按从左到右或从右到左的顺序取出它们的坐标，也就是说我们取出点的坐标值后，再按横坐标值的大小排序。

　　3)让E点的坐标值按我们刚刚取出的点的顺序依次变化，并计算出变化后曲边四边形AFED和曲边四边形EFBC的面积的差值。这样我们就得到一个差值列表。从这个表中挑出面积差值最接近于0的点，则该点就是所求的点。

　　如果最终求出的点的面积差值不符合精度要求，那么可以在第一步取点的时候多取几个，如取10000个。这样就可以保证精度要求。

　　5结论

　　通过以上几个实例我们可以看出：使用UG软件求几何图形的长度和面积非常方便。只要运用得当，UG是就我们手中的一把利剑，很多问题都能迎刃而解，而且迅速和精度高。在这篇文章中我只讲了求长度和面积问题，其实UG是还可以求体积问题的。有兴趣的读者可以自己尝试一下。