在曲面绘制方面,虽然Matlab生成的图形不能直接用于机械设计,但其绘图的机理都是一样的,都是由点生成线,再生成面,区别是Matlab以直代曲,ProE一般生成曲线采用插值,因此,只需要把在MATLAB中绘制的公式曲线、曲面上所有的点坐标数据都提取出来,若能让ProE正确识别,那么我们就可以在其中精确地绘制这些曲线、曲面了。经过尝试,利用Matlab 取得生成曲面需要的数据,将结果存储于. ibl 中,利用ProE 可以直接从. ibl 文件生成曲线这一功能,直接生成曲线,进而生成曲面即可
操作方法,在ProE 中选择“插入”>“基准”>“曲线”或单击基准工具栏上曲线按钮, 选择“从文件”, 然后选择“完成”, 再创建或选择一个曲线参照坐标系, 就可以在出现的窗口中选择要打开的.ibl 文件, 再点击“确定”后曲线就生成了。由.ib l 文件创建曲线的最大优点是改变方便。曲线数据如有改动, 只要修改一下. ibl 文件然后对曲线用“重定义”的方法重新指定文件即可。还有一个优点是可以用一个文件生成多条曲线, 在零件的目录树上可以显得非常简洁。
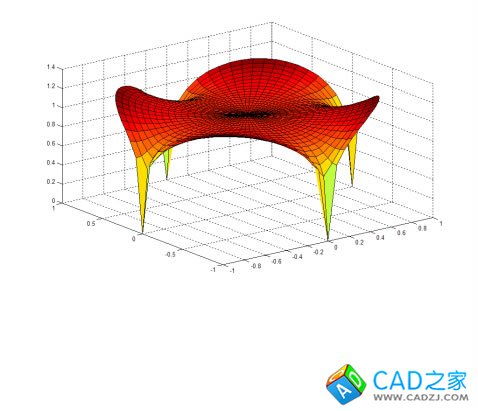
下面是实现过程,以马鞍形为例
(1)利用MATLAB得到公式曲面数据
1)在MATLAB中绘制出曲面
M文件
[th,r]=meshgrid((0:5:360)*pi/180,0:.05:1); %在极坐标系下设置一个73×21的网格矩阵,
[X,Y]=pol2cart(th,r); %转化为笛卡儿坐标系%
Z=X+i.*Y;
F=abs((Z.^4-1).^(1/4));
surf(X,Y,F); %显示曲面的立体图形%
S=[X(:) Y(:) F(:)]; %把X、Y、F 3个矩阵中的数据存储到矩阵S中%
b=size(S);
S=[floor(1:b(1,1));S']';
save flcxq.ibl S -ascii
下面按照ProE生成混合曲线的文件格式对上面生成的结果进行些许修改。
具体参见ProE帮助文档
closed
arclength
begin section
begin curve
1.0000000e+000 0.0000000e+000 0.0000000e+000 1.0000000e+000
2.0000000e+000 5.0000000e-002 0.0000000e+000 9.9999844e-001
3.0000000e+000 1.0000000e-001 0.0000000e+000 9.9997500e-001
4.0000000e+000 1.5000000e-001 0.0000000e+000 9.9987341e-001
5.0000000e+000 2.0000000e-001 0.0000000e+000 9.9959976e-001
6.0000000e+000 2.5000000e-001 0.0000000e+000 9.9902200e-001
7.0000000e+000 3.0000000e-001 0.0000000e+000 9.9796882e-001
8.0000000e+000 3.5000000e-001 0.0000000e+000 9.9622714e-001
9.0000000e+000 4.0000000e-001 0.0000000e+000 9.9353763e-001
1.0000000e+001 4.5000000e-001 0.0000000e+000 9.8958692e-001
1.1000000e+001 5.0000000e-001 0.0000000e+000 9.8399484e-001
1.2000000e+001 5.5000000e-001 0.0000000e+000 9.7629370e-001
1.3000000e+001 6.0000000e-001 0.0000000e+000 9.6589456e-001
1.4000000e+001 6.5000000e-001 0.0000000e+000 9.5203095e-001
1.5000000e+001 7.0000000e-001 0.0000000e+000 9.3366077e-001
1.6000000e+001 7.5000000e-001 0.0000000e+000 9.0928394e-001
1.7000000e+001 8.0000000e-001 0.0000000e+000 8.7656997e-001
1.8000000e+001 8.5000000e-001 0.0000000e+000 8.3148717e-001
1.9000000e+001 9.0000000e-001 0.0000000e+000 7.6578710e-001
2.0000000e+001 9.5000000e-001 0.0000000e+000 6.5626965e-001
2.1000000e+001 1.0000000e+000 0.0000000e+000 0.0000000e+000
......
生成效果图如下;