双曲抛物面的proe建模教程

同样是直纹建模，不过构建出来的部分让你只能管中窥豹，盲人摸象。当然，方法肯定是正确的。

双曲抛物面的直母线运动规律：始终与两条空间交叉的直导线相交，同时平行于一个导平面。

这就是所谓的扭曲面：相邻两素线既不平行，也不相交。

 

 

 

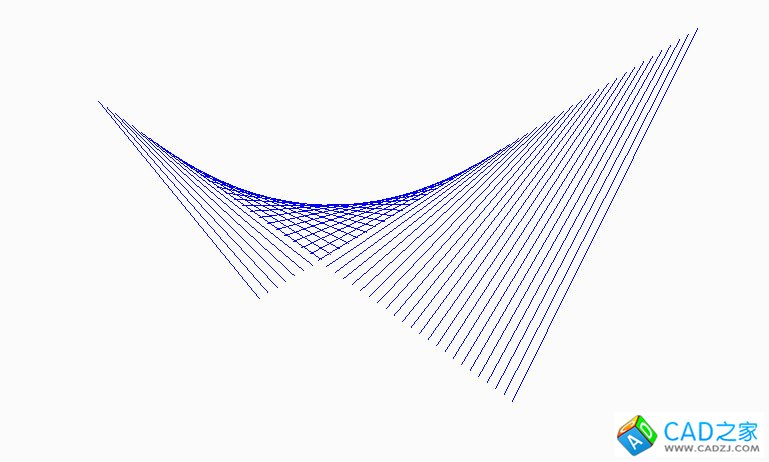
两条导线当然可以处在相互平行的平面内，但是不能够没有夹角。

这么多线，当然也是用阵列了，导平面要先绘制出来，然后以导平面为基础作一基准面，做基准面与两导线的交点，然后以通过点的曲线方式绘制两点曲线。然后把基准面，交点，曲线组成组，这样就可以利用基准面相对导平面的距离来做单方向的尺寸阵列。

双曲线抛物面又叫马鞍面，因为它的全貌是像个马鞍一样的。

那么它的全貌怎样绘制呢？我也没找到什么好方法

下面是我通过不断插入方程曲线的方式绘制的图，这种方式可以说是相当原始的。

曲面交z平面于两条直线，并且通过原点，原点在某种意义上也可以称为这种曲面的心了吧。虽然这种曲面的定义应该是无心曲面。因为两直线是草绘的，而其它双曲线是方程曲线，因此颜色不一样。

 

方程如下：x^2/16 -y^2/9=2z

在proe中，要使用参数方程，所以把方程参数化

z>0的时候
a=4
b=3
sq=sqrt(2*z)

x=a*sq/cos(t*80)

y=b*sq*tan(t*80)

z<0的时候，xy上下对调，ab也上下对调即可。

对z分别取值，给出一些曲线来，可以大略领会曲面的感觉。

z平面上相互交叉的两条直线作为上半部与下半部的分水岭。

称之为马鞍面还是有道理的。

一般的波都是中心向四方发射，这个图，有没有点四方向中心发射波的意味？