基于CosmosWorks的现场铣床结构分析

副标题#e#    0 引言
   
    现场铣床是用于石化装置的现场加工设备。为了适应现场的加工环境，要求现场铣床在满足性能、精度等条件下，其质量和体积尽可能最小。在实际应用中由于横梁的受力变形引起振动，导致工件表面产生了波纹状刀痕，严重影响了加工精度和表面质量。因此，有必要借助有限元软件CosmosWorks，对机床主要移动部件进行静、动态分析。
   
    1 建模与理论分析
   
    1．1实体模型的建立
   
    采用SolidWorks软件建立现场铣床的三维实体模型。铣床在加工时切削力经主轴、主轴箱传递给横梁，主轴箱的重力及悬臂产生的扭矩直接作用于横梁，所以横梁为现场铣床的关键部件，它的刚度直接影响加工精度，因此把横梁、主轴箱作为主要分析的对象。
   
    1．2现场铣床静态和动态特性理论分析
   
    将横梁的结构简化为两点简支梁支承形式，如图1所示(a为横梁中心到主轴箱质心距离)，主轴箱的重力给横梁一力矩M，根据机床运动情况，当主轴箱沿横梁移动到中间位置时，是机床静态刚度最弱的工作状况，静力学分析将选择此时机床的位姿来计算。
   

    首先，进行变量定义，设Fx为切向铣削分力；P为铣削力系数；Sx为工件的移动距离；B为工件宽度；ap为背吃刀量；z为刀具齿数；D为面铣刀直径；m为横梁和主轴箱有限元模型的总体质量矩阵；k为横梁和主轴箱有限元模型的总体刚度矩阵；w为实数，为简谐运动的频率；φ为任意常数。
   
    根据铣削力计算公式，计算出在加工过程中刀具在各方向的受力。
   

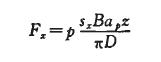
    以直径40 mm的6齿盘铣刀铣削45#钢(调质)工件为例，背吃刀量为5 mm时的进给量为每齿0．2 mm。各铣削分力可由与Fx的比值求得，Fx=1315.2 N，Fy=1808 N，Fx=3123.6 N。其中对加工精度影响最大的是沿Z向分力。
   

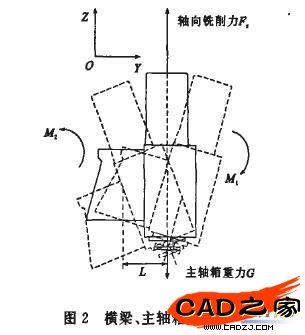
    当铣床处于未工作时状态时，主轴箱的自重G，使横梁受到主轴箱施加的力矩M1。在铣削加工中，铣刀接触工件时，主轴箱受的轴向铣削力E=3123.6 N，主轴箱的重力为G=1986.4 N，E>G，合力作用产生力矩M2，由于横梁刚度不足，使得主轴箱有向上抬起的可能，在铣刀脱离工件时主轴箱受自重回落到原来位置，这样产生了"让刀"现象，如图2所示，导致铣刀平面与工件面呈一角度，当横梁作进给运动时，工件表面产生波纹状刀痕，影响了加工精度。
   

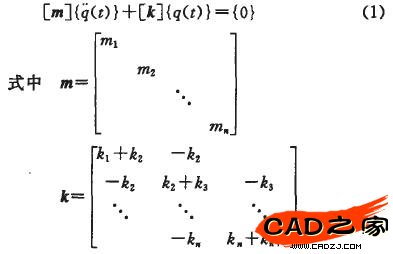
    在横梁和主轴箱振动过程中，可转化n自由度无阻尼系统有限元模型的自由振动方程为：
   

    由于弹性体的自由振动可分解为一系列简谐振动的叠加。因此可设式(1)的解为：
   

    假定系统的质量矩阵与刚度矩阵都是正定的实对称矩阵，可以证明，式(4)的冗个根均为正实根，它们对应于系统的咒个自然频率，这里假定各根互不相等，即没有重根，因而可以由小到大按次序排列为：
   
    将求得的wr(r=1，2，…，n)分别代人式(3)求得相应的"u(r)"这就是系统的模态向量或振型向量。可知各阶固有频率与单位质量的刚度成正比，提高了单位质量刚度也就提高了固有频率。由于激振力的频率一般都不太高，因而只有最低阶的几阶频率才有可能与机床频率接近或重合产生共振。高阶模态的频率已高于可能出现的激振频率，一般不可能产生共振，对于加工质量的影响不大，所以只分析最低阶的几阶模态。