产品设计人员的工作就是,利用各种技术在计算机上勾勒出漂亮的外形,进而设计出魅力十足、激发美感的产品造型。不过,他们所使用的软件工具会用到一些复杂的数学概念,因此,要在计算机上创建出可以吸引眼球的几何外观,用户需要具备相当级别的专业知识才能达到所期望的效果。
对于任何设计造型而言,影响其“美观”程度的最重要的方面就是它的表面:几何形状表面的光滑度、线条和反射度以及不同表面的连接方式,都会影响到可产生美感的物体外观的艺术水准。不过,那些 CAD 和建模软件包总是会提到一些数学方面的专业术语,这就需要那些习惯艺术语言的专业设计人员要领会工具背后的数学原理,而不是奢望自己能够以艺术家的方式来指示软件如何工作。这就是为什么说,掌握与 CAD 软件操作有关的数学知识和常用术语,可以提高产品设计人员将大脑灵感转换为屏幕上完美设计创意的能力。
创建“美观”的表面造型需要用到曲线。还记得微积分吗?您可能想起来了,沿曲线在各点处求导可以获得反映曲线形状的许多信息。这类导数属性通常称为连续性。曲线的一阶导数与曲线的切线有关。切线就是沿曲线绘制的直线。它可以反映出曲线在该点处的方向。一阶导数十分有用,它可以告诉您曲线是否水平,或者告诉您曲线在特定点位置是否与其他曲线的方向一致。沿曲线移动时,如果切线方向不断摆动,则说明该曲线为波浪线。


图 1:曲线的切线和波浪线(切线上下摆动)
二阶导数也很有用,它可以给出特定点处的曲率。这对于准确了解曲线的形状很有帮助。如果曲率由正值变为负值(由凹变凸),就说明存在一个弯曲。"S" 字母的中间部分就是一个弯曲的例子,在该字母中间位置,曲率由一个方向变为另一个方向。图 2 显示了从曲线发出的代表曲线曲率的射线。射线越长,曲率越高。通过这个图示,可以很容易识别出曲线的拐点。 曲率、光滑度和弯曲是确定物体表面是否具有艺术美感的关键因素,因为这些因素对于物体表面如何将光线反射到人眼都有影响。

图 2:弯曲的曲线
三阶导数描述曲率沿曲线变化的加速度或速率。即使像二阶或三阶导数变化的平滑度这样细微的属性都可能会影响到曲线的线条和整体美感。图 3a 显示了具有非连续二阶导数的曲线的曲率迅速变化的一个例子,图 3b 显示了一个具有连续二阶导数的曲线曲率的平滑变化。从设计的角度来看,更需要这种平滑的变化。例如,大部分汽车公司在设计车身时都会避免曲率突变的情况,虽然这种变化似乎微不足道,但通常都会影响到美观性。

图 3a
非连续二阶导数

图 3b
连续二阶导数
同样,这些概念也适用于曲面。曲面的整体形状对于艺术设计来说是最为重要的方面。曲面形状不仅由尺寸和位置决定,而且还受曲面线条、曲率变化率,曲面之间的连接方式等因素的影响。想象一个四方平面,从平面的一边到另一边画几条线,使平面看上去类似于井字棋游戏。跨越平面的这些线称为等参曲线,也就是连接平面相对的两个边上的对应点的曲线。

图 4:等参曲线
可以有多种确定曲面形状特性的方式,但最简单的方法就是沿等参曲线来研究曲面。通过确定等参曲线上各点的导数,可以对曲面及其美观度有一个相当程度的了解。例如,一阶导数可以告诉您任意点处的切线方向。想象在曲面上放一把尺子,使其与某个等参曲线平行。尺子就会指示出它与曲面接触点处曲面切线的方向。这个信息可以帮助确定曲面在该点处是否水平。
二阶导数也会经常用到,因为它可以说明特定点处相对于等参曲线方向的曲率大小。通过沿曲面确定二阶导数,可以了解曲面上哪些部分平坦,哪些部分弯曲。在沿曲面移动时,如果二阶导数的值由正变负或者由负变正,则说明这一部分存在弯曲,即曲面在这里由凹变凸或者由凸变凹。

图 5:弯曲的曲面
曲率和弯曲对于曲面的反光效果和设计方案的整体美感都有很大的影响。还以汽车行业为例,为了达到所需的美观效果,汽车工程师需要花费大量的精力来研究车体的曲率和弯曲。研究二阶导数的变化也非常重要,通过计算三阶导数,可以确定曲率沿曲面的变化速度。人眼会觉察到曲面上存在的非平滑曲率变化,而且能够感觉到这样的变化通常会使曲面缺乏美感。图 6a 显示了曲率平滑变化的曲面。图 6b 显示了曲率非平滑变化的曲面。请注意二者在光线反射效果方面的细微差异。曲率的非平滑变化 (6b) 会沿曲面产生一条比较生硬的反射线。
图 6:曲率平滑变化的曲面与非平滑变化的曲面

6a 曲率平滑变化的曲面

6b 曲率非平滑变化的曲面
另一个重要的设计因素就是曲面之间在公共边处的连接方式。一个可帮助检查曲面连接方式的方法就是使用曲面法线,它是由曲面上的点发出的垂直但远离曲面的矢量。通过比较公共边上各点的曲面法线,可以评测出两个曲面之间的连接是否完美。
拿一个盒子为例,如果各面之间以折角形式相接,数学上将其称为 G0。通过平缘或者圆边相连的曲面称为 G1,因为沿每个曲面公共边的曲面法线是平行的。这些曲面相切。相切的曲面会产生非常美观的造型,比如那些铸件和浇铸出来的产品的表面。不过,人眼可以轻易识别出非平滑的曲率变化,因此,设计人员比较喜欢那种融合在一起的曲面,这样曲面的不仅在公共边上相切,而且它们的曲率也相同。数学上将其称为 G2,而那些公共边在更高阶导数上匹配的曲面连接方式更是广泛应用于汽车和产品设计领域,这种连接使得曲面造型连续、平滑、流畅,令人赏心悦目。图 7 显示了不同级别的连接平滑程度的曲面连接示例。
图 7 小块曲面

G0-折角连接

G1-相切连接

G2-相同曲率连接
在了解有关曲面的设计时,可能会遇到 C0、C1 和 C2 这样的术语。Cn 和 Gn 之间的差异既简单又微妙。如果两条曲线以 G1 方式连接,它们的切向量在连接处平行。如果它们的连接方式是 C1,则其切向量不仅平行,而且量值也相同。获得G1 的效果要比 C1 稍微容易一些。在单个曲面片内产生 Cn 曲面效果很容易达到,但在多个曲面片之间的 C1 和更高程度的连接(多个曲面通过一个边界连接)则要困难一些,需要在曲面内部和边界处颇费一些功夫。有关连接方面的详细说明,请访问 http://en.wikipedia.org/wiki/NURBS。
人眼对物体的反光方式通常十分敏感。设计完美的造型看上去就是舒服,而曲线和曲面连接上存在问题的物体外观显得就是别扭。要找到问题的源头不太容易,但也有办法。有一些工具可以显示出这些细微问题的视觉效果。一个很实用的方法就是通过映射的方式让颜色来反映曲面的曲率。这种方法会显示出曲率的高低以及如何变化。图 8 显示了经曲率映射处理的曲面。

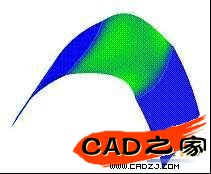
图 8 曲率映射
在图 8a 中,一条清晰的直线标明了曲面从某个曲率(蓝色)变化为更高曲率(绿色)的位置。在图 8b 中,映射图显示了曲面从较低的曲率过度到具有较高曲率的弯曲弧顶的过程。另一种分析工具称为斑马条纹,它能够以夸张的方式显示曲面如何反射光线。

图 9 斑马条纹
专业设计人员花费许多时间和精力来使反射光线产生美观的效果,目的就是使最终产品在消费者看来赏心悦目。了解这些数学概念及其在 CAD 软件中的应用,可以帮助设计人员掌握如何设计出好看产品的技术。所以,下次在看到流光溢彩的漂亮车身时,您就会想到这是设计人员对每一条曲线和曲面精心设计和分析的结果,不仅要考虑整个外形,而且要琢磨车身如何反射来自不同角度的各种光线。有了一双发现美丽的眼睛,再加上对 CAD 软件幕后数学原理的基本了解,设计人员就可以创造出完美的产品造型,它的魅力可能难以言表,但却能产生美感,令人无法拒绝。