阻抗控制在挖掘机器人中的应用与研究

　　一、引言

　　挖掘机器人工作装置的力/位置控制是一个重要课题，对操作臂的柔顺性提出了很高的要求，因此需要对其进行柔顺控制。与被动控制相比，主动控制更灵活，因为控制器参数可以根据需要方便地调节。主动柔顺控制主要有两种：阻抗控制和力/位混合控制。力/位混合控制分别进行力控制和位置控制并可以实现两状态之间的切换，从而实现所需的柔性，但这种柔性是以牺牲系统的鲁棒性为代价的。

　　阻抗控制提供了一个同时适用于自由空间和约束空间的统一框架，具有较少的任务规划工作量。阻抗控制不是直接控制期望的力和位置，而是通过控制力和位置之间的动态关系来实现柔顺功能，使机器人末端呈现期望的刚性和阻尼。

　　二、挖掘机器人工作装置的运动学和动力学模型

　　本文首先在Pro/ENGINEER 4.0中对PC02 -1型挖掘机器人进行实体建模，其结构和参数依据挖掘机器人的物理样机。由于挖掘机器人的操作臂非常重要，因此建模时完全按照物理样机。挖掘机器人的机身复杂，并且对于机器人的控制影响很小，所以采用等效质量法将其简化。设定材料密度为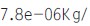，在菜单“分析”→“模型”→“质量属性”中可以求取挖掘机器人工作装置中各连杆的相关质量属性。但是这些参数并不是各关节的动力学参数，需要经过坐标变换处理，得到回转、动臂、斗杆和铲斗的动力学参数。

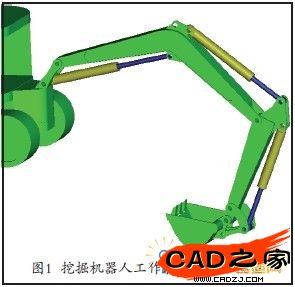
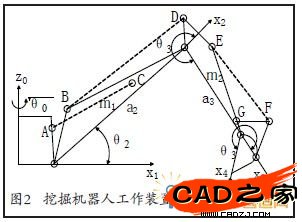
　　挖掘机器人工作装置的运动学方程描述了各工作连杆的关节变量与铲斗尖的位姿(位置和姿态)之间的关系，将各连杆的关节变量与挖掘机器人铲斗的运动轨迹联系起来。图1为挖掘机器人工作装置的实体模型，其连杆坐标简图如图2所示。

　　由关节角求解挖掘机器人铲斗位置和姿态的运动学正解方程为：

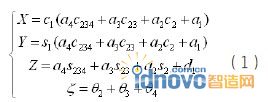
　　其中，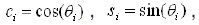

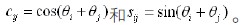
　　考虑挖掘机器人工作时经常使用两自由度情况，即铲斗和斗杆没有相互运动，即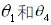均为0，其运动学正解方程可以简化为：

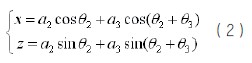
　　由式(2)可得，运动学逆解方程为：

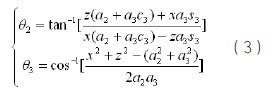
　　操作臂的雅克比矩阵定义为它的操 作速度与关节速度的线性变换。将运动方程两边对时间求导即得出关节变量与位姿变量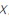之间的微分关系：

　　由上式可以得出雅克比矩阵、转置矩阵、逆矩阵及其导数矩阵：

　　使用拉格朗日法计算挖掘机器人动力学方程：

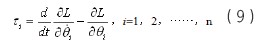
　　由上式推导可得，挖掘机器人的拉格朗日动力学方程一般形式为：

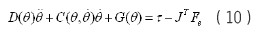
　　其中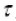为挖掘机器人产生的力矩;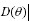为杆件的等效转动惯量;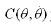为向心力和哥氏矩阵;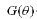为重力项;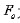为挖掘阻力。

　　对于两自由度的情况，各矩阵分别为：

　　三、阻抗控制策略的应用

　　1.阻抗控制原理

　　阻抗控制通过调整机器人的阻抗参数使力和位置满足某种理想的动态关系，它将力控制和位置控制纳于一个框架之内。在阻抗控制中，期望动力学方程常用二阶动力学、也就是质量-弹簧-阻尼系统表示，现在假设对应于外力，期望的阻抗由下式给出：

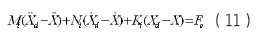
　　其中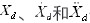分别为期望位置、速度和加速度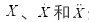，分别为实际位置、速度和加速度。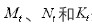分别是惯性矩阵、阻尼矩阵和刚度矩阵。

　　2.阻抗控制的设计

　　在J 可逆的情况下(机构非奇异)求得关节空间的速度向量。对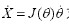求导并整理可得：

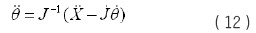
　　把上式代入式(10)得，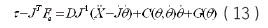

　　令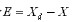，则上式可写为：

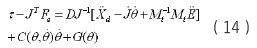
　　把代入上式得

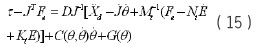
　　整理

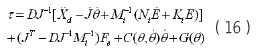
　　如果采用上面的控制律，则可以证实，(11)式的目标阻抗可以实现。

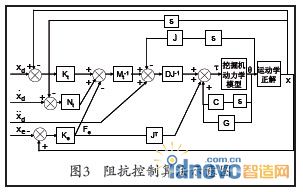
　　根据上面给出的控制律，设计阻抗控制算法流程图，如图3所示。

　　3.阻抗参数对挖掘机器人的意义

　　挖掘机器人在工作过程中，阻抗参数的大小应该根据所装载物料的不同来适当选择。当物料较松软时，可以选用较大的刚度和惯性参数，可以提高工作的效率;当物料较坚硬时，可以选用较小的刚度和惯性参数，以避免对设备造成过载或损坏。至于阻尼参数，它的增大或减小只会使铲斗与物料接触的过程发生变化。为了得到力峰值较小、振荡次数较少且达到稳定时间较短的目的，将其设在使系统处于临界阻尼的状态比较好。