一、引言
自21世纪60年代初激光问世以来,1969年就有人将其用于汽车工业,而随着激光器及外围系统技术的不断进步,激光的使用范围也在不断地扩展。激光切割以其切割范围广、速度高、切缝窄、热影响区小以及加工柔性好等优点而广泛应用于各种加工领域,是激光加工中发展最为成熟的一种技术。在激光加工技术蓬勃发展的今天,激光切割在现代汽车工业、激光加工综合技术和航空航天等领域有着广泛的应用,在我国几乎所有的制造行业中都有钣金加工,例如机床行业、纺机行业、食品机械、电器和仪器仪表等行业。近年来随着全球经济的逐渐复苏和我国国民经济的飞速发展,产业结构的调整使得许多传统产业需要改造,许多钣金加工领域也有待开发,这对三维激光切割钣金件的夹具设计也提出了新的要求。
在三维激光切割加工过程中,由于无切削力,夹具上一般都没有夹紧机构,因此在三维激光切割加工过程中不需要夹紧力,工件的变形主要来自于在不同支撑位置、不同切割路径下的变形以及切割过程中的热变形等。工件的这些变形将造成激光喷头不能垂直于待加工面,以致于切缝粗糙、不平整,甚至造成加工误差无法达到加工要求。在三维激光切割的加工过程中,若工件在自身重力下法向定位不合理或不足,则会造成工件发生翘曲变形,经过三维激光切割后的工件也会随之产生形位误差。因此应该合理地确定工件在法向上的定位,以减小工件在自身重力下产生的翘曲变形,从而减小由其引起的工件切割形状偏差和切口的相对位置偏差。所以在三维激光切割钣金件的夹具设计中,最主要的问题就是根据待加工工件自身的特点,合理地选择最优的定位点个数并确定它们的位置,以实现工件的确定约束定位。本文在“N-2-1”定位原理的基础上,针对待加工工件的自身特点,同时结合三维激光切割的工艺特点,进行相关钣金件在不同支撑情况下的变形研究,从而确定出工件变形最小的支撑定位方案。
二、“N-2-1”定位原理
“N-2-1”定位原理与广泛用于刚性件的“3-2-1”定位原理相比,更适用于易变形薄板类零件的定位。对于柔性件夹具的设计,“N-2-1”定位原理认为 :
(1)第一基准面所需的定位点数为N(N≥3)。
在绝大部分薄板件的加工过程中,最主要的尺寸问题就是薄板件法向方向上的变形,有时自重引起的变形也不容忽视(本文研究的就是钣金件在其自身重力作用下所引起的变形),同时Z向变形会耦合产生另外两个方向上的变形。对于薄板件而言,最合理的夹具系统就是要求其第一基准面上采用多于3个的定位点作为支撑去限制这一方向上的零件变形。
(2)第二、第三基准面所需的定位点数为2个和1个。
在第二、第三基准面上分别需要2个和1个定位点去限制薄板件的刚体运动。2个和1个定位点是完全足够的,因为实际加工力通常不会作用在这两个基准面方向上以避免弯曲或翘曲。同时第二基准面上的2个定位点应布置在薄板件较长的边上。一是由于两定位点间距尽可能大时,零件更稳定;二是可以更好地弥补零件表面或定位元件的安装误差。
(3)禁止在工件正反两侧同时设置定位点,因为甚至是极小的几何缺陷都可能导致薄板件相对巨大的挠度和潜在的不稳定或翘曲,这种现象可利用欧拉翘曲分析来解释。
三、优化设计理论
优化问题的基本原理是通过优化模型的建立,运用各种优化方法,在满足设计要求的条件下迭代计算,求得目标函数的极值,得到最优设计方案。
优化问题的数学模型可表示为:
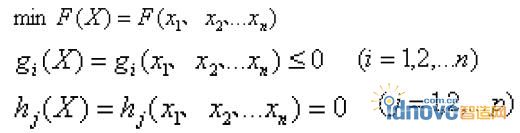
![]()
其中,F(X)为目标函数,是设计变量的函数,用来评价设计方案的优劣,优化问题即为求目标函数的极值。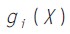 、
、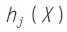 为约束条件,是设计变量取值范围及状态变量的限制条件,也是设计变量的函数。X为设计向量,由设计变量形成,是设计中需优选的设计参数,每个设计向量即为一个设计方案,设计向量的集合为设计空间R,满足约束条件的设计向量的集合为可行域。
为约束条件,是设计变量取值范围及状态变量的限制条件,也是设计变量的函数。X为设计向量,由设计变量形成,是设计中需优选的设计参数,每个设计向量即为一个设计方案,设计向量的集合为设计空间R,满足约束条件的设计向量的集合为可行域。
求解优化问题的方法一般采用数值迭代法如罚函数法(SUMT),将约束优化问题转化为非约束优化问题,通过迭代,逼近目标函数极值。常用的优化方法有零阶方法和一阶方法,零阶方法(直接法)使用所有因变量(状态变量和目标函数)进行逼近,它是通用的方法,可以有效处理绝大多数的工程问题。一阶方法(间接法)同零阶方法一样,通过对目标函数添加罚函数将问题转化为非约束问题,但是与零阶方法不一样的是,一阶方法将真实的有限元结果最小化,而不是逼近数值进行操作。一阶方法使用的是因变量的一阶偏导数,在每次迭代中,梯度计算(用最大斜度法或共轭方向法)确定搜索方向,并用线搜索法对非约束问题进行最小化。一阶方法精度很高,尤其是在因变量变化很大、设计空间也较大时,但消耗的机时较多。#p#分页标题#e#
四、建立三维激光切割钣金件的有限元模型并进行优化分析
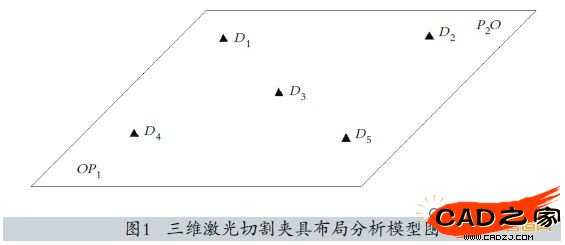
1. 建立三维激光切割钣金件的夹具布局分析模型
在此把钣金件简化成一薄板件进行优化分析,建立其三维激光切割夹具布局分析模型如图1所示,该模型为400×300×1mm的薄板件,材料的弹性模量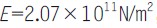 ,密度
,密度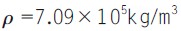 ,泊松比μ=0.3,其中P、P为定位销,定位销
,泊松比μ=0.3,其中P、P为定位销,定位销 应尽量在对角线位置布置,且间距要尽可能的大,这样可以减小激光切割中定位销布局对零件轮廓边切割偏差的影响。在此选择点(40,30)和点(360,270)分别作为两定位销孔的中心。定位销
应尽量在对角线位置布置,且间距要尽可能的大,这样可以减小激光切割中定位销布局对零件轮廓边切割偏差的影响。在此选择点(40,30)和点(360,270)分别作为两定位销孔的中心。定位销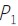 限制薄板件的X和Y向的移动自由度,定位销
限制薄板件的X和Y向的移动自由度,定位销 则限制薄板件绕Z向的转动自由度。
则限制薄板件绕Z向的转动自由度。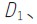
 为B型球头支承钉,用于限制剩下的三个自由度。该类支承钉与工件的接触面积较小,可近似认为与工件是点接触。
为B型球头支承钉,用于限制剩下的三个自由度。该类支承钉与工件的接触面积较小,可近似认为与工件是点接触。
2. 建立有限元模型
在钣金件三维激光切割过程中,工件所承受的载荷主要是工件自身的重力(切割时喷嘴气体产生的对工件的冲击力相对来说很小,可忽略不计),以重力加速度的方式将重力平均加到每个单元上。由于定位销和定位销孔不可能完全紧密地配合,会存在一定的间隙,孔边缘的节点可绕X、Y、Z轴 转动及沿Z方向的移动,所以要限制这些节点的X、Y轴方向的移动自由度。
对于薄板件,一般宜采用具有抗弯曲及扭转特性的shell63壳单元,shell63壳单元可承受与曲面同方向及法线方向的负载。因此分析采用shell63壳单元进行最精细的一级智能网格划分,可得2248个单元。在选择关键点时,1991年R.J.Menassa和W.R.DeVries的研究表明,对于类似薄板零件,最小化在零件边界点和边界中点以及外力作用点处的位移总和是一种比较合理的方案,因此本文选择这9个关键点来构造目标函数。将定位点的位置坐标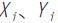 作为设计变量,并使其满足约束条件:
作为设计变量,并使其满足约束条件:
且各关键点的Z向位移量也应满足约束条件:
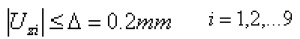
同时将这些关键点的Z向位移量的绝对值作为状态变量,并构造如下目标函数:
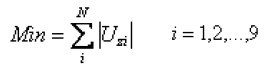
3. 优化分析
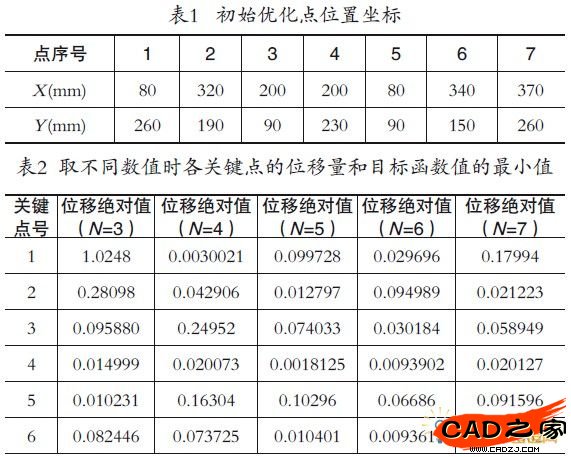
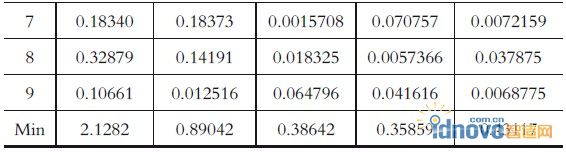
根据初始优化点位置坐标(如表1所示)先进行200步的随机优化,然后在优化结果中选择10个最好的结果进行零阶优化,最大迭代步数设置为200步,最后可得到最优的支撑位置坐标和工件在该位置的Z向变形等值云图。当N取不同数值时,各关键点的位移量和目标函数值如表2所示。
当N=5时,优化定位点的位置坐标和工件的Z向变形等值云图如图2所示。
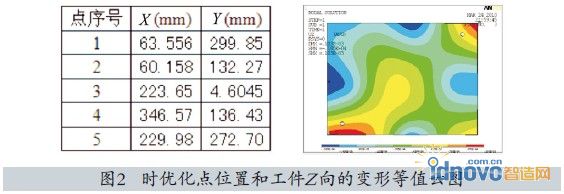
由表2可知,当取N=3时,有3个关键点的位移偏量超过了Δ,所得的目标函数值也较大,因此可知采用“3-2-1”定位原理不能很好地限制工件的变形。当取N=4时,相对于N=3时大多数关键点的位移偏量都有所减小,目标函数值也显著下降,但仍有1个关键点的位移偏量超过了Δ,因此仍需进一步分析比较。当取N=5时,各关键点的位移偏量均小于Δ,符合约束条件,且目标函数较小。而N=6时,大部分关键点的位移偏量变化不是很大,个别关键点的位移偏量还有所升高,目标函数值变化也较小。若采用此方案,则在允许精度范围内由于增加了夹具制造单元,会使夹具的制造成本升高,同时还可能产生误差耦合,因此不宜采用。当取N=7时,虽然仍满足约束条件,但大部分关键点的位移偏量不但没有下降,反而有所升高,目标函数值比N=5和N=6时还要大,这充分说明定位点个数并非越多越好。
由以上分析可得如下结论:当N取5时,能够将工件的Z向变形有效地控制在允许的范围内,且较为经济。所以对于此模型,只要设计出一套由5个夹具单元和2个定位销的夹具布局方案就能取得相对较好的加工效果。#p#分页标题#e#
五、结束语
本文通过采用ANSYS有限元分析软件对钣金件的简化模型——薄板件的支撑位置与其变形关系进行优化分析,得出该模型在三维激光切割的加工过程中最合适的支撑点位置和支撑点个数。为实际应用条件下工件在自身重力作用下的夹具设计,介绍了一种更好的设计方法。该方法不仅可以实现工件较小的变形,使加工顺利进行并达到加工要求,而且还能缩短夹具设计的研发周期、降低设计成本。由于影响工件在三维激光切割加工过程中变形的因素很多,因此在进行夹具设计时还应该综合地考虑各种因素的影响。
相关文章
- 2021-09-08BIM技术丛书Revit软件应用系列Autodesk Revit族详解 [
- 2021-09-08全国专业技术人员计算机应用能力考试用书 AutoCAD2004
- 2021-09-08EXCEL在工作中的应用 制表、数据处理及宏应用PDF下载
- 2021-08-30从零开始AutoCAD 2014中文版机械制图基础培训教程 [李
- 2021-08-30从零开始AutoCAD 2014中文版建筑制图基础培训教程 [朱
- 2021-08-30电气CAD实例教程AutoCAD 2010中文版 [左昉 等编著] 20
- 2021-08-30电影风暴2:Maya影像实拍与三维合成攻略PDF下载
- 2021-08-30高等院校艺术设计案例教程中文版AutoCAD 建筑设计案例
- 2021-08-29环境艺术制图AutoCAD [徐幼光 编著] 2013年PDF下载
- 2021-08-29机械AutoCAD 项目教程 第3版 [缪希伟 主编] 2012年PDF