稳定ＣＯ２焊焊接电流模糊控制器的设计与仿真

  焊接电流是影响焊丝熔化和焊缝熔深的主要焊接参数，一般在焊接过程控制中常作为恒定的设定参数来考虑。通常焊接电流是由送丝特性曲线与焊接电源外特性交点所决定的，在调节外特性曲线位置而调整电弧电压时，焊接电流就会随电压值的变化而偏离原来的设定值。焊接电路和电弧电压这两个主要的规范参数之间的关系是一种非线形的耦合关系，利用人工想很快使焊接电流回复到原设定值是很困难的［１］。另外，由于网络电压的波动、保护气体纯度、流量以及焊炬高度的变化等都引起焊接电流的波动。虽然焊机本身具有的自身调节作用，但都会给焊接电流带来一定的误差。针对以上情况，本文研制了一种以可编程控制器(ＰＬＣ)为核心器件并自主开发的软件，实现稳定行ＣＯ２焊焊接电流的模糊控制器。
  模糊控制器具有良好控制效果的关键是具有一个完善的控制规则。但对于高阶、非线性、大时滞、时变以及随机干扰严重的复杂被控过程，仅靠对操作者实践经验的总结或模糊控制信息的归纳，很难设计出适合被控过程不同运行状态的控制规则。
  为此，本文不采用Ｍａｍｄａｎｉ规则表，而是在基本模糊控制器的设计基础上，设计了一种带修正函数自寻优模糊控制器(如图1)，

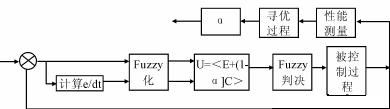
它是一种自组织的模糊控制器［２］；并对所设计的模糊控制器使用ＭＡＴＬＡＢ（含ＳＩＭＵＬＩＮＫ）软件进行仿真。 

  ２ 模糊控制器的设计 

  ２．１ ei,ei/dt和ui基本论域的确定
  由送丝特性曲线可知，当焊接电流在短路与过渡(小规范)范围内，电压每秒变化一伏，电流变化在几安培之内，当进行中规范焊接时，电弧电压变化一伏，电流变化最大可达十几安培。
  本程序把ei在小规范论域设定为［－１０～＋１０Ａ］；ei在中规范论域设定为［－３０～＋３０Ａ］；ei在大规范论域设定为［－６０～＋６０Ａ］。
  在ＰＬＣ系统中ei/dt可以写为［ｅ（ｋ）－ｅ（ｋ－１）］／Δｔ。Δｔ是指扫描时间，对于某一个确定的程序而言，扫描一次的时间是相同的，因此可以把它设为一个常数，用［ｅ（ｋ）－ｅ（ｋ－１）］的大小近似地代表dei/dt.［e(k)-e(k-1)］的范围可估计为：０≤｜［ｅ（ｋ）－ｅ（ｋ－１）］｜≤２ｍａｘ［｜ｅ（ｋ）｜－｜ｅ（ｋ－１）｜］，所以可以取dei/dt的基本论域分别为：［－２０Ａ／ｓ＋２０Ａ／ｓ］；［－６０Ａ／ｓ＋６０Ａ／ｓ］；［－１２０Ａ／ｓ＋１２０Ａ／ｓ］。
  为了便于编写程序，对小、中、大的ei和ei/dt的论域分别给上一个合适的比例因子ｋ１、ｋ２、ｋ３。取：ｋ１＝３ ｋ２＝１ ｋ３＝１／２；得到ei和ei/dt的统一的格式为［－３０，＋３０］，［－６０，＋６０］。
  ei是每次采集得到的u(k)与给定值之差，所以ui的论域可取与ei的相似论域，即为［－３０，＋３０］。
  ２．２ 输入输出的语言变量
  在工程实际中，语言变量权ｍ一般取为５～１０档，结合本系统的具体的性能，本控制器取为５档。离散的语言变量论域中元素个数ｎ与ｍ的关系为：ｎ＝（１．５－２）ｍ，因此ｎ可取为9，从而ei,ei/dt和ui的语言变量论域E,Ec,U分别为：
  ［－４，－３，－２，－１，０，＋１，＋２，＋３，＋４］
  与此对应偏差量化因子为０．１；偏差变化率量化因子为０．０５；输出量化因子为０．１。
  ２．３ 模糊控制器的规则
  假设被控对象的实际动态过程可用下式描述：
  Ｙ（Ｋ）＋ａ１Ｙ（Ｋ－１）＋…＋ａｎＹ（Ｋ－ｎ）＝ｂ１Ｕ（Ｋ－ｍ－１）＋…ｂｎＵ（Ｋ－ｍ－ｎ）＋ｅ（Ｋ）＋ｃ１ｅ（Ｋ－１）＋…＋ｃｎｅ（Ｋ－ｎ） （１）
  式中Ｕ（Ｋ），Ｙ（Ｋ）分别为被控对象的输入和输出；ｅ（Ｋ）为噪声干扰率明表示被控对象的传输延时；ａｉ，ｂｉ，ｃｉ（ｉ＝１，２，…ｎ）为各项系数。#p#分页标题#e#
  设计一个预报模型，即根据Ｋ时以前的数据Ｙ（Ｋ），Ｙ（Ｋ－１），…和Ｕ（Ｋ），Ｕ（Ｋ－１），…来预报Ｙ（Ｋ＋ｍ＋１），其中ｍ＝０，１，２，…。根据自适应控制理论，预报模型的方程为：
  Ｙ（Ｋ＋ｍ＋１）＋α１Ｙ（Ｋ）＋…αｐＹ（Ｋ－ｐ－１）＝β０Ｕ（Ｋ）＋β１（Ｋ－１）＋…＋βＵＬ（Ｋ－Ｌ）＋∈（Ｋ＋ｍ＋１） （２）
  式中∈（Ｋ＋ｍ＋１）为预报模型的偏差，令向量ＸＴ（Ｋ）＝［－Ｙ（Ｋ），－Ｙ（Ｋ－１），］…－Ｙ（Ｋ－ｐ＋１），Ｕ（Ｋ－１），…，Ｕ（Ｋ－Ｌ）；
    定义参数向量θＴ＝［α１，α２，…，αｐ，β１，…，βＬ］，则式(2)
可简化为：Ｙ（Ｋ）＝β０Ｕ（Ｋ－ｍ－１）＋ＸＴ（Ｋ－ｍ－１）θ＋∈（Ｋ） （３）
  对于参数向量θ的估计，可以采用简单的最小二乘递推法，其递推形式为：
  θ（Ｋ＋１）＝θ（Ｋ）＋Ｒ（Ｋ）［Ｙ（Ｋ）－β０Ｕ（Ｋ－ｍ－１）－Ｘ（Ｋ－ｍ－１）θ（Ｋ）］
  Ｒ（Ｋ）＝Ｐ（Ｋ）Ｘ（Ｋ－ｍ－１）［１－Ｘ（Ｋ－ｍ－１—）Ｐ（Ｋ）Ｘ（Ｋ－ｍ－１）］－１?
  Ｐ（Ｋ＋１）＝Ｐ（Ｋ）－Ｐ（Ｋ）［１＋ＸＴ（Ｋ－ｍ－１）Ｐ（Ｋ）Ｘ（Ｋ－ｍ－１）ＲＴ（Ｋ）］ （４）
  式中，θ（Ｋ）和θ（Ｋ＋１）表示在Ｋ和（Ｋ＋１）采样时刻的参数向量θ的估计量
；Ｐ（Ｋ）是ｍ×ｍ阶矩阵，它的维数取决于未知参数的数目，而与测量次数无关。
  因此，可由式(4)求出Ｙ（Ｋ）的预报值，从而求出预测误差ｅ和误差的变化率ｅｃ。若给定值为Ｒ，则：
  ｅ＝Ｙ（Ｋ）－Ｒ，ｅｃ＝Ｙ（Ｋ－１）－Ｙ（Ｋ） （５）
  将ｅ和ｅｃ整量化及模糊化后，可得带有调整因子的规则可调的Ｆｕｚｚｙ控制规则：
  Ｕ＝－［αｅ＋（１－α）ｅｃ］ （６）
  式中，Ｕ为控制量Ｕ的整量值；α为调整因子，又称加权系数，α∈（０，１）。
  α值的大小，直接反映了对偏差ｅ和偏差变化率Δｅ的加权程度。因此，上式通过调整单一因子的值，就可以很方便地修改控制规则，以改善系统的控制效果。但这种规则的单因子自调整方法存在一些不足，就是其控制规则只依赖一个α参数；一旦确定α，则偏差ｅ和偏差变化率Δｅ的权重就确定了。在实际中控制系统处于不同工作状态时，要求ｅ和Δｅ的权重不同；当ｅ的绝对值较大时，控制系统的主要矛盾是消除ｅ，故此时应增大α值，使ｅ在控制规则中占较大的权重，以改善系统的动态特性；当ｅ的绝对值较小时，控制系统的主要矛盾是抑制系统超调，使系统尽快达到稳态，故此时应减小α值，而１－α值则相应增大，使Δｅ在控制规则中占较大的权重。用单因子调整控制规则显然无法实现系统状态变化的需要。
  为了克服单因子自调整的不足，根据偏差的量化值的大小，提出了一个多因子自调整控制规则的算式：
  采用带修正因子的控制规则，即使是采用五因子修正算式，α（ｉ＝１－５）值选取仍有较大的盲目性，往往是先凭经验预定出α的若干个不同的取值，再逐一对它们进行实验仿真，以选择最优值。这种方法既耗时又繁琐，而且往往选不到真正最优的α值。因此还需要设计一种修正因子自寻优的模糊控制器，它能在系统控制过程中对α进行实时自寻优，以实现控制规则的自调整和自完善，达到提高控制系统品质的目的。
  带修正因子自寻优的模糊控制系统结构如图1所示，其中通常是取：Ｊ＝∫∞０ｔ｜ｅ｜ｄｔ为目标函数，并以目标函数的值为最小作为系统的性能指标，而且用修正因子α为寻优参数。寻优过程是针对被控过程的运行状况，根据目标函数值的大小不断地对因子α进行修正，使目标函数值逐步减小，直到系统的控制性能达到要求为止。若运行状况发生新的变化，则需重新执行寻优过程，直到调整出适合新运行状态设为修正因子。#p#分页标题#e#
  在对给定的输入响应求目标函数值时，由于用计算机组成的模糊控制系统是一个离散系统，故应把目标函数Ｊ化为离散算式：
  Ｊ＝Σ〖ＤＤ（〗?ｎ〖〗ｉ＝１〖ＤＤ）〗ｉＴ｜ｅ（ｉ）｜Ｔ?＝Σ〖ＤＤ（〗?ｎ〖〗ｉ＝１〖ＤＤ）〗ｉＴ?２｜ｅ（ｉ）｜〖ＪＺ）〗〖ＪＹ〗（８）
  其中：Ｔ是采样周期，ｉ是采样序号。
  如果把采样周期T看成单位时间，则可取Ｔ＝１。式(8)可写为：
  Ｊ＝Σ〖ＤＤ（〗Ｎ〖〗Ｉ＝１〖ＤＤ）〗ｉ｜ｅ（ｉ）｜〖ＪＺ）〗〖ＪＹ〗（９）
  这样，只要先凭经验选择一组初始修正因子α＝｛α?１，α?２，α?３，α?４，α５｝，得出一组初始的控制规则来对被控对象进行控制，然后对系统响应的过度过程进行采样，即可用式(9)求出目标函数Ｊ的值。
  在求得系统的目标函数值后，在应用寻优算法进行修正因子α的在线自寻优，使目标函数值Ｊ?＝ｍｉｎ或达到给定值为止。此时的?α??＝｛α?１??，α?２??，α?３?，α?４??，α?５??｝为最优修正因子，系统的特性也达到了最优，其中的寻优算法可采用单纯算法(其方法在自动控制理论相关的书籍上都有介绍)。
  ２．４ 模糊控制表的完成
  当选用不同的修正因子时，根据公式(7)就会得到不同的模糊控制规则而形成不同的模糊控制表。对于弧焊电源这样一个典型的被控对象，其传递函数假定为：Ｇ（ｓ）＝１／ｓ（ｓ＋１）。设给定的输入为单位阶跃输入信号，现采用修正因子自寻优方法对以上对象进行控制。为了得到最优的α值，首先凭经验预定出5个不同的取值α?１＝０．３，α?２＝０．４，α?３＝０．５，α?４＝０．６和α?５＝０．７；再以式(9)表示的J为寻优目标，采用单纯形法作为寻优方法，经过多次调整最终找到Ｊ＝ｍｉｎ的最优修正因子为：?α?１??＝０．２８，α?２??＝０．５０，α?３??＝０．６６，α?４??＝０．７９，α?５??＝０．９３。?
  ２．５ 模糊控制输出量的反模糊化
  将上面得到的控制量的论域乘以比例因子，便可得到实际的控制增量，加上原来的控制量，输出去控制被控对象。若在(4)的基础上，不对输入输出量进行量化，而对所得到的一组优化修正因子进行曲线拟合，得到修正因子的连续表达式，则可获得连续的输出量。对修正因子进行拟合运算的模糊控制系统见图1。这样可消除量化误差和调节死区。
  综上所述，带修正因子的自组织模糊控制器可以抛开控制表，把模糊控制规则综合成一个简单算式，直接求取控制量，并可以根据系统的运行状态，通过调整α值，很方便地进行在线调整控制规则，以改善系统的控制性能。因此这是一种既方便又有效的自组织模糊控制器，特别适合于工程上应用。 

  ３ 模糊控制器的仿真和分析

  由于模糊控制器的设计思想是模拟人脑的思考过程，在模糊控制器的设计过程中，对实际经验的依赖性很大，要求设计者结合实际经验，选取控制量，设计控制规则。选取的某些控制量和控制规则的效果如何，必须编制大量的程序进行仿真分析，或者是等到控制器完成以后通过实际来观察、验证。显然，这两种方法都费时费力，而且都必须通过大量实验才能确定，实际设计过程中，类似的工作往往占总工作量的大部分。针对上面的情况，本文使用ＭＡＴＬＡＢ(含ＳＩＭＵＬＩＮＫ)软件进行仿真。
  ３．１ ＳＩＭＵＬＩＮＫ中的模型的创建方法
  一般模型元件的创建，关键在S函数的正确编制及调用。S函数实质上是具有特殊调用格式的ＭＡＴＬＡＢ函数，表征系统动态特性，能使ＳＩＭＵＬＩＮＫ有能力构造一般的仿真方框图，灵活方便的设计出用户的特殊环节。
  实际上，ＳＩＭＵＬＩＮＫ的每一个模型都可以用输入、输出、状态三个要素进行描述：
  ｆｕｎｃｔｉｏｎ［ｓｙｓ，ｘ０］＝ｓｆｕｎｃ（ｔ，ｘ，ｕ，ｆｌａｇ，参数1，参数2，…）??［３］?#p#分页标题#e#
  其中，ｓｆｕｎｃ是用户定义的系统，ｔ是当前时刻，ｘ是当前状态值，ｘ０是初始状态值，ｕ是当前系统输出值，变量ｆｌａｇ的值返回变量ｓｙｓ的信息。
  模糊控制原理如图1所示。其中具有调整因子的模糊控制环节，用S函数描述如下：
  zt fuzzy.m
  function［sys,x0］=zt fuzzy(t,x,u,flag,ke,kc,ku,a)
  if abs(flag)=3
  E=round(ke*u(1));
  C=round(ke*u(2));
  Sys=ku*(a*E (1-a)*c);
  Else if flag=0
  Sys=［0;0;1;2;0;0］;
  Elae
  Sys=［］；
  End
  将上述S函数进行成组(Group)和封装(Mask)处理，就得到用户创建的ＳＩＭＵＬＩＮＫ模块。在系统仿真中新模块与ＳＩＭＵＬＩＮＫ提供的标准模块功能完全一样，具有相同的仿真效率及可信度。
  ３．２ 模糊控制器的仿真及分析
  将上述S函数经过封装处理后，在ＳＩＭＵＬＩＮＫ模型库中找出与设计的系统相对应的模块，把它们拖到新模型窗口中，用线连接起来就可以创建一个如图2示的模糊系统模型图。

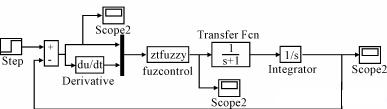
  利用该模型就可以对所设计模糊控制系统进行仿真研究。图中ＺＴＦＵＺＺＹ模块是自建的
  模糊调节器模型，图中step是仿真时输入的阶跃信号，焊接电流的传递函数假设为：?Ｇ（ｓ）＝１／ｓ?（ｓ＋１）?，图中的示波器ｓｃｏｐｅ的作用是实时的画出控制系统的输出结果曲线，也可以将数据存储到ＭＡＴＬＡＢ的工作空间中，再利用绘图ｐｌｏｔ命令将输出曲线在单独窗口画出来。
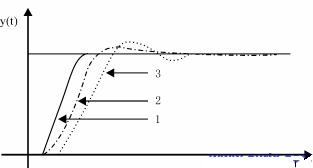
  采用多修正因子的自调整规则进行控制仿真的结果如图3所示。其中曲线3对应于五个修正因子α?１＝０．３，α?２＝０．４，α?３＝０．５，α?４＝０．６和α?５＝０．７时控制系统的单位阶跃相应，曲线2应于五修正因子α?１??＝０．２８，α?２??＝０．５０，α?３??＝０．６６，α?４??＝０．７９，α?５??＝?０．９３?时控制系统的单位阶跃相应，而曲线1是系统在线调整修正因子时控制系统的相应曲线。由图可见，离线优化的因子(曲线2)的控制较未优化(曲线3)的控制效果要好，而在线调整因子(曲线1)控制效果最好，超调最小，相应时间最短。但由于在线优化给控制器增加了负担，使实时效果降低。

  ４ 结论

  1)所设计的稳定ＣＯ?２焊焊接电流模糊控制器不仅可以有效的消除电弧电压调节过程中所引起的焊接电流的偏差，而且也可以消除网络电压波动、保护气体纯度或流量以及焊炬高度变化所引起的偏差。
  2)设计焊接电流的带修正函数自寻优模糊控制器的稳定性好，阶跃响应的超调小，动态响应快。