CNC系统中任意空间曲线的插补方法
时间:2011-05-20 08:43:10 来源:未知
在CNC机床上加工工件,无论是加工曲面还是曲线,加工过程的刀具中心轨迹都是曲线。传统的CNC机床只能加工简单的直线和圆弧等曲线,加工复杂的曲线需要在编程时转化为简单曲线。随着计算机技术的发展和机械零件复杂程度的提高,人们希望CNC机床能直接加工任意空间曲线。尤其样条曲线的发展,这种希望更迫切。本文运用数据采样时间分割法和泰勒(Taylor)公式,推导出一种任意参数曲线的等速进给实时插补算法。下面给以介绍。
1 参数曲线插补算法
一般曲线c可写成如下形式
c(u)={x(u),y(u),z(u)} uÎ[u0,un]
(1)
u是任意参数,通常0≤u≤1。大多数CAD/CAM系统采用参数形式表示曲线。用参数描述曲线有以下优点:参数形式曲线对于控制多轴机床是非常方便的,每个轴可以单独驱动。另外,曲线上点的计算容易,这是由于x,y,z都是参数u的显函数,故易于计算。
CNC系统插补器的任务是在恒插补周期T(T是常数,一般为1~10ms)内计算输出一次由下式确定的进给弦长DL(uk)在x,y,z轴上的坐标分量
DL(uk={x(uk+1)-x(uk),y(uk+1)-y(uk),z(uk+1)-z(uk)}
k=1,2,…,n-1
(2)
CNC系统要求每次插补所形成的弦长相等,因此,实时插补方法不能建立在参数的等分上,而应建立在每个进给步长DLk相等的基础上。现在的关键是推导出弦长相等的条件下相应的参数增量Duk。以下是恒速进给实时插补算法的具体推导。
沿参数曲线的进给速度可按下式计算
V(u)=
ds
=(
ds
)(
du
)
dt
du
dt
(3)
(4)
其中s为曲线的自然参数即弧长,有
ds
=[(x')2+(y')2+(z')2]½
dt
(5)
x'=
dx
y'=
dy
z'=
dz
du
du
du
式(4)要求ds/du≠0,由式(5)知,即要求该曲线为正则曲线。
把式(5)代入式(4),得
花少量的时间计算式(6)的解是实时插补算法的关键,然而V为常值条件下的解u(t)一般难以求得。因此,不妨在t=kT处使用泰勒(Taylor)级数展开进行迭代求解。由泰勒公式得
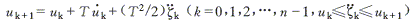 (7)
(7)
最后一项为一阶泰勒公式的余项,是二阶无穷小量,对于插补计算可忽略不计。把式(6 )代入式( 7 ) ,忽略二阶余项,得
uk+1=uk+
VT
(x'2+y'2+z'2)½
(8)
由式(8 )确定uk+1代入式(1 )和式(2 )即可计算出插补步长DL((u )k)的各个坐标分量。该算法的优点就是保证插补点始终在曲线上,无累积误差,只有弓高误差。
2 最大插补步长和弓高误差的关系
由以上恒速实时插补算法推导可知,插补点始终在曲线上,无累积误差,因此弓高误差就是插补误差。弓高误差d受给定精度指标e的限制,即必须有d≤e。实际加工的弓高误差取决于插补步长DLk 、曲线的曲率k和挠率t。k和t由下式决定。
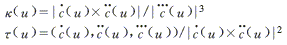 (9)
(9)
(10)
由于插补步长很短,因此可将被插补弧看作半径为Rk的圆弧。这样的简化是偏安全的。Rk由下式决定
Rk=1/max(k(ui),t(ui)) (k,i=0,1,2,…n-1;uk≤ui≤uk+1
(11)
那么,DLk逼近曲线弧DCk的弓高误差dk如图1所图。图1中,DLk和dk之间的关系可表达为
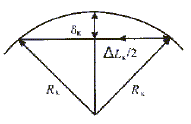
图1 弓高与步长的关系
若对任意t∈[0,1] ,要求插补器输出由式(2 )给定的 DLk逼近对应的曲线弧DCk时,弓高误差对所有k均有#p#分页标题#e#dk≤e,则最大插补步长可表示为
式(13 )中R由下式决定
R=1/max[max(k(u)),max(t(u))] u∈[u0,un]
(14)
式(14 )可由参数方程(1)代入式(9 )、式(10 ) ,分别用普通函数求最大值的方法得到。
3 结束语
本文介绍的插补方法能用在所有以参数方程表示的任意空间曲线上。这些曲线可包括B样条等所有样条曲线。计算的复杂程度也不是很高,一般带浮点运算器的计算机都能胜任,加之插补时间固定,能很好地满足控制系统对实时性的要求。
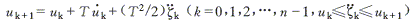 (7)
(7)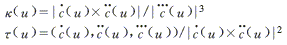 (9)
(9)