一、前言
二、复合角度锪刀刃磨运动模型
- 机床坐标系
- 刃磨空间复合角度刀具的机床一般需设置5个坐标(3个移动坐标和2个转动坐标)。典型的机床坐标系如图2a所示,其中X轴为机床工作台纵向移动,Y轴为机床溜板(或砂轮头架)横向移动,Z轴为砂轮头上下移动,c轴为机床圆工作台(水平转台)的转动,d轴为工件主轴(刀具轴线)的转动。X、Y、Z轴的移动相互垂直并相互独立,水平转台位于机床工作台之上并随工作台一起运动,其轴线与Z轴相一致,工件主轴位于水平转台之上并随水平转台一起转动,其轴线与水平转台轴线垂直相交,其交点设为坐标系原点。为了使刀具准确定位,刀具安装在工件主轴上的位置应能调整。通常工件主轴支座安装在小滑板上,移动小滑板,可使刀具沿工件主轴轴线方向(u向)移动。
- 角向位置计算
- 设刀面i的单位法矢量为
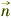 i(见图3),则有:
i(见图3),则有:
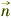 i=[
i=[ xni ]=[ cosgoisinbHi ] yni cosgoicosbHi zni singoi (1) - 式中goi为刀面i法矢量的方向余角(与XOY坐标平面的夹角);bHi为刀面i法矢量在XOY坐标平面上的投影与Y轴夹角。
 图1 气门口复合角度锪刀
图1 气门口复合角度锪刀- 若采用碗形砂轮刃磨(图2b),且令砂轮工作平面与Y轴相垂直,则刃磨刀面i时应使其法矢量与Y轴的反方向相一致。为此可由图2b的位置出发进行下面的两次旋转:
- 令刀具绕自身轴线(此时为X轴)转wd角,使刀面i的法矢量转至XOY平面(第4象限)上,显然有:
wd=-arctan( zni ) yni (2)
- 经此旋转后,
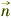 i转至
i转至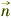 'i的位置:
'i的位置:
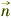 'i=[
'i=[ x'ni ]=[ xni ] y'ni ynicoswdi-znisinwdi z'ni ynisinwdi+znicoswdi 
图2 机床坐标系与刀具刃磨起始位置
(3) - 经此旋转后,
- 令刀具绕Z轴转wc角,使刀面i的法矢量转至Y轴位置,应有:
wci=arctan( x'ni ) y'ni (4) - 例如,在图2b所示位置上,刀面I的法矢量与XOY平面的夹角go1=5°,其在XOY平面上的投影与Y轴的夹角bH1=150°,由式(1)、(2)、(3)、(4)可分别求出:
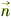 1=[
1=[ 0.499 ];wd1=3.463°; 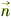 '1=[
'1=[ 0.499 ];wc1=-29.955° -0.865 -0.866 0.053 0 - 同理可求出其它刀面由刃磨起始位置(图2b所示位置)转至刃磨位置的转角wd和wc。
- 空间坐标计算
- 取刀面上一点P,其矢量表示为:
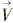 p=[
p=[ xp
yp
zp] - P点与刀具一起绕自身轴线(图2b位置为X轴)转wd角后,
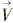 p变为
p变为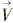 p1:
p1:
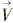 p1=[
p1=[ xp1 ]=[ xp ] yp1 ypcoswd-zpsinwd zp1 ypsinwd+zpcoswd (5) 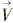 p1绕Z轴转wd角后,变为
p1绕Z轴转wd角后,变为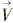 p2:
p2:
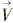 p2=[
p2=[ xp2 ]=[ xp1coswc-yp1sinwc ] yp2 xp1sinwc+yp1coswc zp2 zp1 (6) - 例如,刀面I上P1点在图2b所示位置的矢量为:
 图3 刀面法矢量
图3 刀面法矢量 - 取刀面上一点P,其矢量表示为:
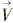 p=[
p=[ 56.440
-11.751
0] -
- 经绕自身轴线(X轴)旋转wd1,再绕Z轴旋转wc1后得到:
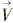 p2=[
p2=[ 43.044
-38.344
-0.710] - 经绕自身轴线(X轴)旋转wd1,再绕Z轴旋转wc1后得到:
- 机床各轴运动量
- 刀面i由刃磨初始位置移至刃磨位置,各坐标轴的运动量如下:
{ Dxi=xPR-xpi2
Dyi=yPR-ypi2
Dxi=zPR-zpi2
Ddi=wddi
Dci=wcdi(7) - 式中xPR、yPR、zPR为刃磨初始位置砂轮上参考点的坐标,xpi2、ypi2、zpi2为刀面i上对刀点由刃磨初始位置经绕自身轴线(X轴)旋转wdi角,再绕Z轴旋转wci角后的坐标。式(7)即可理解为空间复合角度刀具刃磨运动模型。
- 刀面i由刃磨初始位置移至刃磨位置,各坐标轴的运动量如下:
- 设刀面i的单位法矢量为
三、复合角度锪刀的刃磨
| Rw=[ | 48 -22.5 0 |
] |
| 项目 | 刀面 | ||||
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | ||
| 原始参数 | g0(刀面法矢量与XOY平面夹角)(°) | 3 | 15 | 3 | 15 |
| bH(刀面法矢量在XOY平面投影与Y轴夹角)(°) | 150 | 150 | 110 | 110 | |
| x0(刀面上对刀点x坐标)(mm) | 56.44 | 56.44 | 52 | 52 | |
| y0(刀面上对刀点y坐标)(mm) | -11.751 | -11.721 | -9.974 | -9.897 | |
| z0(刀面上对刀点z坐标)(mm) | 0 | 0.5 | 0 | 0.5 | |
| 刃磨参数 | wd(绕X轴转角)(°) | 3.463 | 17.192 | 8.712 | 38.076 |
| wc(绕Z轴转角)(°) | -29.955 | -28.879 | -67.785 | -65.186 | |
| Dx(X轴补偿量)(mm) | 4.956 | 4.058 | 39.284 | 33.529 | |
| Dy(Y轴补偿量)(mm) | 15.844 | 14.692 | 29.704 | 28.098 | |
| Dz(Z轴补偿量)(mm) | 0.71 | 2.987 | 1.511 | 5.71 | |
四、结论
- 本文以气门口锪铰刀为例,说明了空间复合角度锪刀数控刃磨的原理与方法,该方法也同样适用于其它空间复合角度刀具的数控刃磨。
- 本文所述方法的核心是运用矢量方法计算所需刃磨的刀面由刃磨初始位置运动至实际刃磨位置机床各轴的运动量,按此运动量编制数控加工程序,即可实现空间复合角度刀具的数控刃磨。
- 上述原理和方法,在普通工具磨床上配置精密转台和分度头,也可以实现空间复合角度刀具的刃磨。
相关文章
- 2021-09-08BIM技术丛书Revit软件应用系列Autodesk Revit族详解 [
- 2021-09-08全国专业技术人员计算机应用能力考试用书 AutoCAD2004
- 2021-09-08EXCEL在工作中的应用 制表、数据处理及宏应用PDF下载
- 2021-08-30从零开始AutoCAD 2014中文版机械制图基础培训教程 [李
- 2021-08-30从零开始AutoCAD 2014中文版建筑制图基础培训教程 [朱
- 2021-08-30电气CAD实例教程AutoCAD 2010中文版 [左昉 等编著] 20
- 2021-08-30电影风暴2:Maya影像实拍与三维合成攻略PDF下载
- 2021-08-30高等院校艺术设计案例教程中文版AutoCAD 建筑设计案例
- 2021-08-29环境艺术制图AutoCAD [徐幼光 编著] 2013年PDF下载
- 2021-08-29机械AutoCAD 项目教程 第3版 [缪希伟 主编] 2012年PDF