插齿数字化共轭曲面修形

　　长期的生产实践和理论分析都表明：对齿轮沿齿廓和齿向作适当的修形，可以消除啮合冲击和齿向载荷集中，齿间载荷分配更加合理，齿向载荷分布更加均匀，啮合噪音降低，传动更加平稳[1-3]。近年来，齿轮修形技术已广泛应用于各种重要齿轮传动。目前的齿轮修形一般通过刀具修形或磨削成形来获得最后修形表面。这样的方法效率低、成本高、加工柔性差，而且质量、精度难以控制。对于多联齿轮和内齿轮，则无法实现修形加工。随着数控加工技术的发展，采用数控机床加工齿轮及齿面修形的技术日益获得重视。数控加工齿轮修形克服了传统加工方法的缺点，能够保证高精度的要求。本文研究齿轮修形的数控加工规律，提出采用标准插齿刀在三轴数控插齿机上实现齿轮的齿廓修形加工方法。

　　1 数字化共扼曲面求解及数控插齿修形加工分析

　　非数控的普通插齿机，其刀具与齿坯的展成运动是定速比运动，由渐开线齿形的刀具展成出渐开线的齿廓。如果要采用渐开线齿形刀具加工出偏离渐开线的修形齿廓，则必须根据修形齿形在任意时刻改变瞬时相对运动速比。因此，本加工方法必须在数控插齿机上才能完成，而特定时刻的瞬时相对运动速比是由刀具和被加工齿廓的共扼关系所确定的。要获得数控编程所需要的运动参数，首先需要进行共扼关系的分析计算。在早期的修形齿廓中，大多数都是解析表达的，而基于有限元边界元等方法的齿廓修形计算，所给出的结果通常是离散的。解析表达的可以离散为数值表达，因此，解决数字化齿面共辗求解，就解决了所有的修形齿面共扼求解问题，归结起来，就是首先要解决数字化共扼曲面求解问题。

　　数字化共扼曲面原理研究由离散点集描述的数字化曲面与数字化曲面之间，或数字化曲面与共扼解析曲面之间的联系与运动及其相互转化规律。数字化共扼曲面原理脱胎于传统的解析理论，应用现代数值方法，离散数学以及计算机对数据离散处理的能力，将宏观的连续曲面共扼问题转化为微观的离散共扼问题[4]。

　　如图1所示，一对共扼曲面要满足两个条件：

　　图1 两曲面的共轭运动

　　对于齿轮的数控插齿修形，由于只考虑齿廓修形，因此可简化为二维数字化修形齿面与刀具齿面之间的共扼运动[5]。如图2所示，o-xy为固定坐标系，o1-x1y1为与插齿刀相固联的动坐标系，o2-x2y2是与二维数字化齿面相固联的动坐标系，op-xpyp为辅助坐标系，图3表示插齿刀的齿形。在坐标系o1-x1y1中，插齿刀上的任意一点坐标P(x1，y1)，该点处斜率为k1，在坐标系o2-x2y2中修形齿面上的一点P’(x2，y2)，该点处斜率为k2。当插齿刀转动φ1，被加工齿轮转动时φ2时，P和P’处于共扼接触。

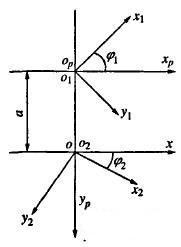
　　图2 数控插齿加工坐标系

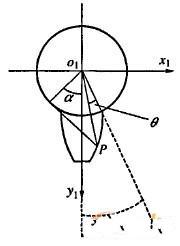
　　图3 插齿刀齿形

　　在固定坐标系下P和P’满足下列共扼条件：

　　在上述方程组中，已知数字化修形齿面上一点的坐标x2，y2和斜率k2，而插齿刀上任意一点的坐标x1，y1及斜率k1可由插齿刀在此点的压力角来表示，即x1=x1(α1)，y1=y1(α1)， k1=k1(α1)，且中心距α也为可求。故此方程组为三元非线性方程组，未知参量为φ1，φ2，α1这3个。通过数值解法即可解此方程组。φ1为插齿刀的旋转运动，φ2为齿坯的旋转运动。这样，由代表数字化齿面的数字化点的一组参数x2，y2，k2可唯一确定一组α1，φ1，φ2，从而唯一确定了插齿刀具形成面上与数字化齿面点(x2，y2)共扼的一点(x1，y1)以及这一对共扼点达到接触位置所需的两个离散共扼运动φ1，φ2。

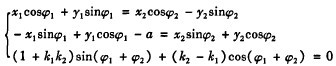
　　已知插齿刀齿形和修形齿面的数字化点坐标及其斜率，都可以求解求插齿刀和修形齿面的相互运动，而且求解精度也达到要求。如果仅知道修形齿面的坐标点，则可以通过样条插值或Hermite插值求出各点的斜率。

　　齿廓修形包括齿顶修形和齿根修形。一般情况下，为了保证齿根弯曲强度，只对齿顶进行修形，特殊情况下才会对齿顶和齿根均进行修形。齿廓修形有3个重要参数：修形量，修形长度和修形曲线。当这3个参数确定以后修形曲线就可以确定了，然后对其进行离散，就可以得到二维数字化修形齿面。

　　插齿刀是一组各段剖面为不同变位系数的变位齿轮的叠加，但插齿加工中起作用的是前端面。由于插齿刀在使用中前端面不断磨损，因此在修形加工前要测出插齿刀前端面的实际变位系数。可以实测出插齿刀前端面的公法线长度Wk，再由下式计算[6]。

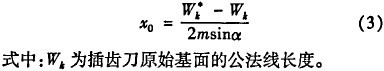
　　2 运动求解及数控编程

　　当插齿刀和修形齿面确定以后，就可以对其进行运动求解。一般情况下，所求得的插齿刀和齿轮运动的传动比是时刻变化的。在三轴数控插齿机上，即插齿刀和工件的圆周运动的传动比可以时刻变化，这就使在数控插齿机上加工修形齿面成为可能。

　　实际加工是以时间参数t为变量的连续加工，必须将离散展成共扼运动插值成连续共扼运动。对于每一个φ2，对应一个φ1和其一阶导数P，若给定n个插值节点φ2=φ21，φ22，…，φ2n，则对应有φ1=φ11，φ12，…，φ1m和P=P1，P2，…，Pn。则连续运动φ1=(φ2)可用分段Hermite插值求得。其插值密度由数控加工系统相应轴的分辩率决定。

　　在φ2∈[φ2，k，φ2，k+1]区间上，φ1(φ2)的表达式为

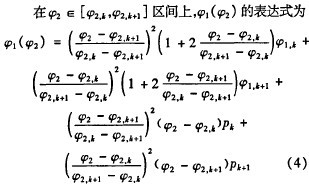
　　令k=1，…，n-1，则在φ2∈[φ2，1，φ2，n]，可求得φ1(φ2)∈[φ1，1，φ1，n]，即φ1(φ2)是给定区间的连续函数。

　　令

　　φ2=w2t(w2=const) (5)

　　有

　　φ1=φ1(φ2)=φ1(w2t)=φ1(t) (6)

　　φ2(t)，φ1(t)即为实际展成齿面二个运动轴的真实运动。

　　得到两个轴的运动数据后就可以按其运动编写数控代码。在加工中可以按从修形起点到齿顶点的顺序进行修形，也可以按相反顺序进行修形。与加工渐开线齿轮不同的是，由于在修形加工中改变了定比传动关系，插齿刀转动相对变慢，因此只能逐侧齿廓进行修形，即修完一侧齿廓后再加工另一侧齿廓。

　　3 加工干涉分析

　　用标准渐开线插齿刀实现齿廓修形，在工件齿顶渐开线成形段，因重合度大于1的影响，插齿刀与工件一般处于双齿成形啮合切削区，这样如果仍按照常规的啮合展成齿形的传动规律来展成修切齿廓1的齿顶时，势必干涉破坏另一齿廓2的根部形状，干涉仿真如图4和图5所示。

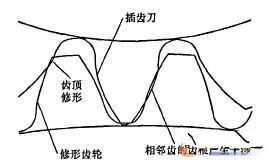
　　图4 修形加工干涉

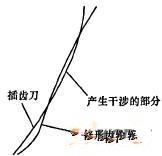
　　图5 干涉放大图

　　为解决这一问题，可采取的措施：

　　(1)对齿顶和齿根同时修形，且要求在双啮合区齿顶的齿根的修形相匹配，即双啮合区中一齿廓的齿顶与另一齿廓齿根的成形切削同时完成。

　　(2)如果只对齿顶进行修形，则可以采用中心分离的办法。即增大插齿刀与被加工齿轮的中心距，使修形加工中重合度始终小于1，则插齿刀一直处于单齿啮合状态，因此修形过程中不会产生对相邻齿的加工干涉。中心分离的距离可以按重合度小于1计算，最直接的办法是以插齿刀的齿顶点来加工修形部分的起点，通过这两个点的共扼关系就可以确定中心分离以后的中心距。此时，加工中首先要先加工出标准的渐开线齿轮，对齿轮的修形要作为一个独立的工序放在加工的最后一步完成。

　　4 加工实验研究

　　4.1 加工实验

　　实验已知条件：插齿刀齿数z1=18，被加工齿轮齿数z2=18，模数mn=6，压力角α=20°，插齿刀前端面公法线测量值，=46.05，插齿刀的齿顶高系数h=1，3，齿轮修形曲线为圆弧，齿轮修形量dmax=45um，齿轮修形长度hmax=6mm(为使修形更明显，实验时取较大的修形参数)。在被加工的齿轮修形部分取巧个型值点，并按数字化共扼曲面原理进行运动求解，如表1所示，并将所得运动进行插值，如表2所示。

　　表1 插值实验数据

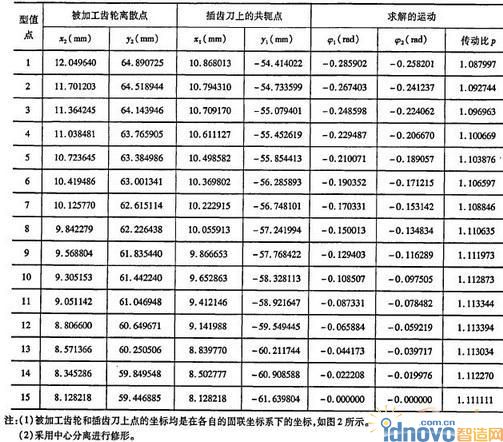
　　表2 插值后两个数控轴的运动数据

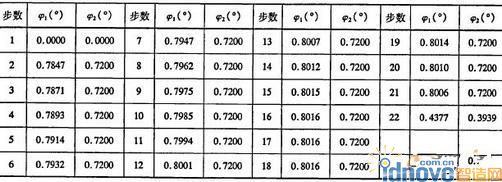
　　为了保证加工精度，运动插值要有比较小的步长;而从表2中可以看出加工修形的运动数据与加工渐开线齿轮的定比传动运动数据相差很小，并且修形量越小，差异越小。由于数控机床的最小增量单位为0.001°或0.0001°，如果步长较小，当差异小于0. 0001度时，就会和加工渐开线齿轮的运动一样，不能正确的加工修形齿轮。因此在插值时必须选取合适的步长，并且数控机床的最小增量单位最好选为0.0001°。

　　4.2 修形齿廓的检验

　　实验加工的修形齿轮如图6所示。为了检验修形效果，需对该齿轮进行测量。本实验中插齿机的加工精度为7级，查资料得该齿轮的允许齿廓偏差Fm=19μm[7]。参照渐开线齿形的测量方法，对修形齿廓的检验方法有两种：

　　(1)在渐开线齿形测量仪上测量。由于一般齿形测量仪是用来测量渐开线齿轮的，因而测量修形齿轮要考虑修形部分的影响。本实验在SP-60渐开线测量仪上测量3个齿面，测量结果如图7所示，从图中可以看出修形齿轮的齿廓曲线的走势与修形曲线基本符合。3个齿面的齿面偏差分别为-60.1 μm，-57.8μm和-50.5μm，除去修形量45μm的影响，因此所加工的修形齿轮的齿廓精度满足要求。

　　图6 数控插齿加工的修形齿轮

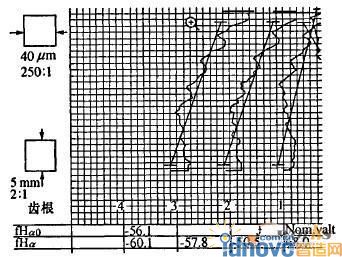
　　图7 在渐开线测量仪上测量修形

　　(2)在三坐标测量机上测量。如图8、图9所示，对加工后的修形齿廓进行坐标测量，图形显示实际修形齿廓与理论修形齿廓匹配较好。对测量数据进行数据处理和图形匹配后，经计算得齿廓误差为17.6μm，符合精度要求。

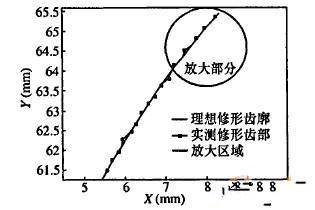
　　图8 实测修形齿形与理想修形齿形对比

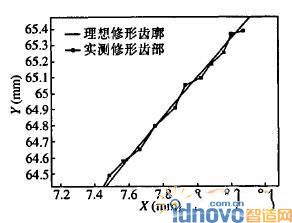
　　图9 齿形对比放大部分

　　实验证明本论文提出的数字化齿面展成方法及其相应算法应用于数字化渐开线修形齿轮的加工是正确的和可行的。

　　5 结论

　　齿轮特别是高速重载齿轮，其轮齿修形技术应用相当广泛。本文根据数字化共扼曲面原理，通过主动控制插齿刀和工件间的成形切削运动关系，来实现任意齿廓的修形。采用标准插齿刀在数控插齿机上就可以加工出修形齿轮，与传统加工修形齿轮时首先对齿轮刀具进行修形相比，大大缩短了修形齿轮的设计周期。由于CNC系统控制运动的柔性，数控插齿修形可适用于各种形状和参数的齿廓修形，从而为修形齿轮的设计、制造及推广提供了新的技术手段。数控插齿修形是一项新技术，它将齿轮设计与齿轮制造集成一体，为齿轮产品进人计算机集成化制造创造了条件。