用ANSYS有限元分析软件求解

1 用ANSYS分析软件求解Hertz问题

    假设两个球体1和2接触，它们的半径分别为：R1=10mm,R2=15mm;弹性模量E1=220GPa,E2=69Gpa;泊松比为V1=0.27,V2=0.3;球1顶部施加集中载荷Q=8000N。

    根据轴对称关系，按照轴对称平面接触模型进行计算，见图1。

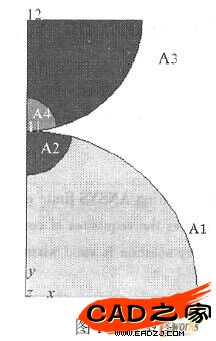
    对接触体进行四边形有限元划分，在接触区域附近其节点编号如图2所示。

应当注意，在划分单元之前，一定要预先估算加载后接触区域的大小，否则可能使划分的单元大于接触区域尺寸，从而不能精确计算出（甚至无法计算出）接触区的尺寸。一般情况下，单元尺寸尽可能小，应使其为接触椭圆半径的1/3左右。当然也不能无限制地细化单元，以免导致计算机的计算时间增加。适宜的单元大小划分过程要经过反复调试。

    有限元接触应力求解结果见图3。ANSYS求解结果和Hertz理论解的比较列于表1中。在提取节点载荷时，如果节点载荷Fy>0,则该点处于接触状态（在模型最上端施加了负y向的力），否则处于非接触状态。最大法向应力则应该是所有接触点应力的最大值。接触区域的半径应为最远的那个接触点的x坐标值与该点x方向位移值之和的绝对值，即R=|X+Ux|.

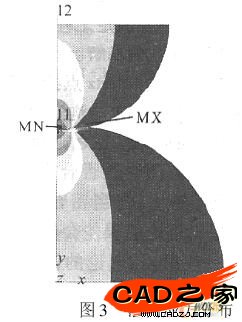
    结果比较在表1中列出。其中aA,σA是接触半径和最大接触应力的ANSYS解，ah和σh是其Hertz理论解。

    比较的结论是，两者求解的结果非常接近，接触尺寸误差仅为1.52%，而最大应力误差也仅为3.09%。因此可以说，用ANSYS软件求解接触问题有足够的精度，是可靠的。

   2 Hertz 点接触理论的适用范围以球和球窝接触为例，分别用Hertz理论和ANSYS求解。

如图4所示，钢球直径Dw=2mm,球窝的曲率半经为r（给定一系列数据），小球顶点施加集中载荷Q=20N；两接触体物理参数为E=207GPa。同上面的例子一样，建模、划分网格、设置参数和接触对。ANSYS解和Hertz理论解的接触半径与最大应力结果比较见表2。由于材料是轴承钢，故在本例中Hertz点接触理论公式可用

    从表2可以看出，当f≥0.54时，Hertz理论解和ANSYS解基本一致，接触尺寸误差和最大应力误差分别为2.40%与4.63%；当f<0.54时，误差会越来越大；当f=0.52时，两者的误差分别为4.99%与8.41%。此时Hertz理论的结果已不十分可靠了，而球轴承的情况正好与此相似。当f更小时，Hertz理论已基本失效。