副标题#e# 随着计算机辅助设计制造技术的飞速发展,计算机仿真技术已成为工程技术人员极其重要的科研工具,文中利用计算机仿真技术精确地绘制出摆线轮的齿廓曲线,简化了摆线轮齿廓的绘制过程,研究结果对提高摆线轮设计的速度和质量具有一定的实际意义。
COSMOSMotion是为广大用户提供的实现数字化功能样机的优秀工具,它与当今主流的三维CAD软件SolidWorks无缝集成,是全功能的运动仿真软件,可以建立各种复杂运动机构的精确运动模型,并对运动机构进行完整的运动学和动力学仿真,得到机构中各零部件的运动数据,分析机构中零件的位移、速度、加速度、作用力与反作用力等,并以图形、动画、表格等多种形式输出运算结果。大大简化了机构的设计开发过程,缩短了开发周期,减少了开发费用,同时又提高了产品质量。总之,COSMOSMotion功能强大,求解可靠,仿真结果与实际情况十分吻合,完全能够满足用户对运动仿真的各种需求。
作为普通减速机的更新换代产品,摆线针轮行星减速器与普通减速机相比,具有结构紧凑、传动比大、传动效率高、多齿啮合、承载能力大等突出优点。摆线针轮行星减速器以其输入输出同轴、多齿啮合的新颖结构,广泛应用于矿山、冶金、工程机械及化工等行业的驱动装置和减速装置中瞄J。摆线针轮传动采用圆柱面针齿与具有短幅外摆线等距曲线齿面的摆线轮相啮合,摆线轮齿面形状极为复杂,但对整个系统的承载能力与精度有极大影响,因此齿面的造型也极为重要。摆线轮的齿廓形状因其特殊性给加工制造增加了难度,至今其齿廓还不能实现共轭切削加工,因此摆线轮的加工必须由齿廓外形图来提供支持。利用COSMOSMotion的仿真功能可以很精确地将摆线轮的齿廓形状表达出来,所以,探讨利用COSMOSMotion进行摆线轮的三维设计方法具有实际的意义。
1 摆线轮齿廓曲线成形原理
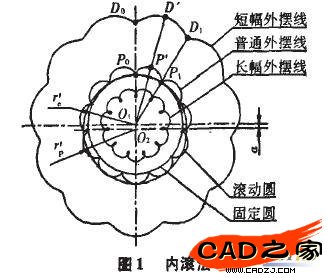
齿廓成形原理是绘制齿廓曲线的依据,形成外摆线的方法有内滚法和外滚法。内滚法如图1所示,以半径为ro的圆作固定圆,用半径为rp的圆作为滚动圆套在固定圆外面,两圆的半径差就是其中心距,即a=rp-ro。当滚动圆绕固定圆滚过全周长2πrp时,与滚动圆同步滚动的任何一点均可形成一条完整的外摆线,这种形成外摆线的方法称为内滚法。如果该点位于滚动圆的圆周上(如图1中的Po点),由Po点形成的外摆线Po P P1。称为普通外摆线。当该点位于滚动圆之外时(如图1中的Do点),由现点形成的外摆线莉。称为短幅外摆线,比值Kt=rp/O2D0称为短幅系数。当该点位于滚动圆以内时,其轨迹为长幅外摆线。
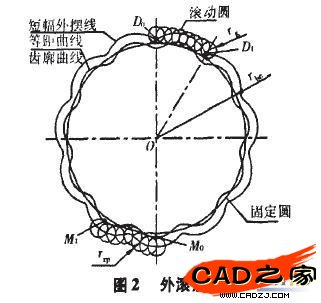
外滚法如图2所示,在图2中使半径为rg的滚动圆G沿半径为,rbc的固定圆J作纯滚动,当滚动圆G沿固定圆.,滚过一周时,滚动圆内一点仇描绘出的轨迹DoD1是一条短幅外摆线,短幅系数为K1=ODo/rg。当滚动圆G沿固定圆J滚过2πrbc距离时,仇点描绘出的轨迹就是一条完整的摆线轮廓。
在摆线针轮行星齿轮传动中,摆线轮是以短幅外摆线DOD1作为理论齿廓的,而固定针轮以Do点作为理论齿形。但是,实际针齿不可能做成一点,必须做成半径为,。的圆柱形。因此,以摆线轮的理论齿廓上各点为圆心,以k为半径作圆,这些圆的内包络线眠麝。就是摆线轮的实际齿廓,又称为短幅外摆线的等距曲线。而针轮的实际轮廓就是半径为k的圆(如图2所示),滚动圆中心所在圆的直径为2rp,rp为滚动圆中心所在圆的半径,也就是滚动圆G与固定圆J的中心距,即rP=rg+rbc。满足以下3个条件时,采用外滚法形成的短幅外摆线与采用内滚法得到的短幅外摆线相同:
2 摆线轮齿廓曲线绘制方法
由于摆线轮齿廓曲面形状的特殊性,有关其齿形轮廓设计方法的技术资料并不多。在摆线针轮传动中,摆线轮齿廓的形状误差直接影响摆线针轮的传动精度和传动系统的运行寿命。摆线轮齿廓曲面的绘制关键在于摆线轮廓曲线的绘制,只要精确地绘制出摆线轮廓曲线,摆线轮齿廓曲面的三维造型即迎刃而解。
摆线轮的齿廓曲线是一种比较复杂的函数曲线,无法采用常规的造型方式。而利用COSMOSMotion的轨迹跟踪功能,可以根据摆线轮齿廓曲线成形原理,通过简单的运动仿真,即可精确地绘制出摆线轮廓曲线。下面通过具体实例详细介绍具体绘制过程。
COSMOSMotion是为广大用户提供的实现数字化功能样机的优秀工具,它与当今主流的三维CAD软件SolidWorks无缝集成,是全功能的运动仿真软件,可以建立各种复杂运动机构的精确运动模型,并对运动机构进行完整的运动学和动力学仿真,得到机构中各零部件的运动数据,分析机构中零件的位移、速度、加速度、作用力与反作用力等,并以图形、动画、表格等多种形式输出运算结果。大大简化了机构的设计开发过程,缩短了开发周期,减少了开发费用,同时又提高了产品质量。总之,COSMOSMotion功能强大,求解可靠,仿真结果与实际情况十分吻合,完全能够满足用户对运动仿真的各种需求。
作为普通减速机的更新换代产品,摆线针轮行星减速器与普通减速机相比,具有结构紧凑、传动比大、传动效率高、多齿啮合、承载能力大等突出优点。摆线针轮行星减速器以其输入输出同轴、多齿啮合的新颖结构,广泛应用于矿山、冶金、工程机械及化工等行业的驱动装置和减速装置中瞄J。摆线针轮传动采用圆柱面针齿与具有短幅外摆线等距曲线齿面的摆线轮相啮合,摆线轮齿面形状极为复杂,但对整个系统的承载能力与精度有极大影响,因此齿面的造型也极为重要。摆线轮的齿廓形状因其特殊性给加工制造增加了难度,至今其齿廓还不能实现共轭切削加工,因此摆线轮的加工必须由齿廓外形图来提供支持。利用COSMOSMotion的仿真功能可以很精确地将摆线轮的齿廓形状表达出来,所以,探讨利用COSMOSMotion进行摆线轮的三维设计方法具有实际的意义。
1 摆线轮齿廓曲线成形原理
齿廓成形原理是绘制齿廓曲线的依据,形成外摆线的方法有内滚法和外滚法。内滚法如图1所示,以半径为ro的圆作固定圆,用半径为rp的圆作为滚动圆套在固定圆外面,两圆的半径差就是其中心距,即a=rp-ro。当滚动圆绕固定圆滚过全周长2πrp时,与滚动圆同步滚动的任何一点均可形成一条完整的外摆线,这种形成外摆线的方法称为内滚法。如果该点位于滚动圆的圆周上(如图1中的Po点),由Po点形成的外摆线Po P P1。称为普通外摆线。当该点位于滚动圆之外时(如图1中的Do点),由现点形成的外摆线莉。称为短幅外摆线,比值Kt=rp/O2D0称为短幅系数。当该点位于滚动圆以内时,其轨迹为长幅外摆线。
外滚法如图2所示,在图2中使半径为rg的滚动圆G沿半径为,rbc的固定圆J作纯滚动,当滚动圆G沿固定圆.,滚过一周时,滚动圆内一点仇描绘出的轨迹DoD1是一条短幅外摆线,短幅系数为K1=ODo/rg。当滚动圆G沿固定圆J滚过2πrbc距离时,仇点描绘出的轨迹就是一条完整的摆线轮廓。
在摆线针轮行星齿轮传动中,摆线轮是以短幅外摆线DOD1作为理论齿廓的,而固定针轮以Do点作为理论齿形。但是,实际针齿不可能做成一点,必须做成半径为,。的圆柱形。因此,以摆线轮的理论齿廓上各点为圆心,以k为半径作圆,这些圆的内包络线眠麝。就是摆线轮的实际齿廓,又称为短幅外摆线的等距曲线。而针轮的实际轮廓就是半径为k的圆(如图2所示),滚动圆中心所在圆的直径为2rp,rp为滚动圆中心所在圆的半径,也就是滚动圆G与固定圆J的中心距,即rP=rg+rbc。满足以下3个条件时,采用外滚法形成的短幅外摆线与采用内滚法得到的短幅外摆线相同:
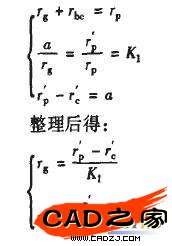
2 摆线轮齿廓曲线绘制方法
由于摆线轮齿廓曲面形状的特殊性,有关其齿形轮廓设计方法的技术资料并不多。在摆线针轮传动中,摆线轮齿廓的形状误差直接影响摆线针轮的传动精度和传动系统的运行寿命。摆线轮齿廓曲面的绘制关键在于摆线轮廓曲线的绘制,只要精确地绘制出摆线轮廓曲线,摆线轮齿廓曲面的三维造型即迎刃而解。
摆线轮的齿廓曲线是一种比较复杂的函数曲线,无法采用常规的造型方式。而利用COSMOSMotion的轨迹跟踪功能,可以根据摆线轮齿廓曲线成形原理,通过简单的运动仿真,即可精确地绘制出摆线轮廓曲线。下面通过具体实例详细介绍具体绘制过程。

相关文章
- 2021-09-08BIM技术丛书Revit软件应用系列Autodesk Revit族详解 [
- 2021-09-08全国专业技术人员计算机应用能力考试用书 AutoCAD2004
- 2021-09-08EXCEL在工作中的应用 制表、数据处理及宏应用PDF下载
- 2021-08-30从零开始AutoCAD 2014中文版机械制图基础培训教程 [李
- 2021-08-30从零开始AutoCAD 2014中文版建筑制图基础培训教程 [朱
- 2021-08-30电气CAD实例教程AutoCAD 2010中文版 [左昉 等编著] 20
- 2021-08-30电影风暴2:Maya影像实拍与三维合成攻略PDF下载
- 2021-08-30高等院校艺术设计案例教程中文版AutoCAD 建筑设计案例
- 2021-08-29环境艺术制图AutoCAD [徐幼光 编著] 2013年PDF下载
- 2021-08-29机械AutoCAD 项目教程 第3版 [缪希伟 主编] 2012年PDF