有限元分析在各个工程领域得到了广泛的应用,有限元法程序包亦成为CAD常用计算方法库中不可缺少的内容,并与优化设计形成了集成系统。应用这些计算分析方法.设计人员可高效合理地寻找最佳设计方案。通过利用三维CAD软件SolidWorks中的有限元分析工具COSMOS对联轴部件中的连杆进行分析及结构优化设计。
一、前言
CAD(Computer Aided Design计算机辅助设计)的一个重要特征是提供了对新产品模型进行分析、综合与评价的数值求解方法。当把设计对象描述为计算机内部模型后,研究如何使产品达到性能要求、进行新产品技术指标的优化设计、性能预测、结构分析仿真的数值求解方法称为CAE(Computer Aided Experiment计算机辅助分析),这种方法已成为CAD/CAM (Computer Aided Manufacturing计算机辅助制造)集成中不可缺少的工程计算分析技术。该技术中的核心计算方法是一种有效的数值分析方法一有限元分析。
本文中要利用有限元分析进行结构优化设计的零件是联轴部件〔图1)中的连杆。联轴部件是应用在液压气动自控部件中的一个组成部分,在外力作用下,连杆带动轴作周期转动,转动中推杆"联轴部件之外的零件)始终与轴中间不规则截面部分保持接触,使得推杆上下运动,从而控制电磁阀开、关的动作。连杆为联轴部件中传递外力的主要零件,材料为合金钢,控制端在φA处与键及轴连接,承受外力在φB处。该零件的毛坯是铸件。改进前的结构要保证连杆φA孔与其一侧平面有较高的垂直度,才能确保联轴部件中的连杆在带动轴旋转的过程中.侧平面不会与端盖接触,造成转动不流畅的现象,同时,连杆作为一个传动零件,从经济性角度考虑,本身结构应当灵巧一些。改进后的结构会不会影响在承受相同外力情况下零件的强度。这是本文利用有限元分析进行连杆的结构优化设计的重要部分,准确地说,能否肯定新的结构,有限元分析在零件的优化设计中起到了至关重要的作用。

二、有限元分析
1有限元法的基本概念
有限元法(Finite Element Method,简称FEM)是一种数值离散化方法,根据变分原理求其数值解。因此适合于求解结构形状及边界条件比较复杂、材料特性不均匀等力学问题能够解决几乎所有工程领域中各种边值问题(平衡或定常问题、动态或非定常问题),如:弹性力学、弹塑性问题疲劳与断裂分析、动力响应分析、流体力学、传热、电磁场等问题。
有限元法的基本思想是:在对整体结构进行结构分析和受力分析的基础上,对结构加以简化,利用离散化方法把简化后的边界结构看成是由许多有限大小、彼此只在有限个节点处相连接的有限单元的组合体。然后,从单元分析人手,先建立每个单元的刚度方程,再用计算机对平衡方程组求解,便可得到问题的数值近似解。用有限元法进行结构分析步骤是:结构和受力分析一离散化处理一单元分析一整体分析一引人边界条件求解。

2.有限元分析的前置处理
建立有限分析模型的过程,即前置处理是有限元分析的关键环节。前置处理的功能主要包括:离散化网格模型的自动生成、网格的修改、拼接和节点编号的优化、载荷及材料数据的建立、边界条件的定义(零位移、已知位移、接触、磨擦等约束条件的处理)、模型数据检查与编辑修改、模型的图形显示等。在对机械结构进行有限元分析时,还要对所分析的结构进行简化,正确分析其受力情况,并对约束条件进行有效的处理,以便建立一个合理,正确的有限元计算模型。
建立计算力学模型的第一步是作结构分析和受力分析,合理地确定单元类型.对大型复杂结构,往往要选用多种单元进行组合模拟。在结构分析时,简化是必需的,但不能因简化而失真,导致计算误差增大。利用有限元分析问题时的简化方法与原则是:结构中对结果影响不大、但建模又比较复杂的特殊区域是简化的主要对象,同时明确简化后对计算结果带来的影响是有利还是没利。例如对图2a所示的连杆结构进行有限元划分时,附着肋板可用梁单元模拟,其余部分则按板元处理,有限元分析网格划分。为计算简便,也可以直接将此结构简化为平板来考虑(图26),有限元分析网格划分。需注意的是简化过程并不是简单地去掉这些加强肋板。正确的简化方法是采用等刚度原则进行等效处理,使原结构与简化后的结构能在相同的受力状态和边界条件下,各节点产生相同的位移,即两者具有相同的刚度。
由于实际应用中机械结构常常很复杂,即使对结构进行了简化后,仍难用单一的单元来描述.因此在对机械结构进行有限元分析时,必须选用合适的单元并进行合理的搭配,如:杆状单元;薄板单元。多面体单元等。这样就可以使所建立的计算力学模型能在工程意义上尽量接近实际结构,提高计算精度。
单元划分时应充分利用结构的对称性,以确定是以整个结构.还是取部分结构作为计算模型来分析求解。例如图2a所示的连杆中间部分可以看作受纯弯曲的梁,它对连杆的中心轴对称,而载荷也对中心轴对称。可见,应力和变形亦将具有同样的对称特性。所以只取连杆中间部分来计算就可以了.通过对连杆有限元分析后,将其删去部分结构(图26)的影响可以这样考虑:处于轴对称面内各节点的方向位移为0,处于轴反对称面上各节点的的方向位移亦为0。这样,在图36中相应节点处可安置限制方向位移的约束是为了消除刚体位移而设置的。
有限元软件在几何建模完成以后便进行自动化网格划分,但没有考虑到边界条件和载荷分布情况对离散化过程的影响。自适应网格划分技术,通过吸取专家分析经验,将边界条件与载荷状况作用于网格划分过程,对关键区域的网格进行局部细化,实现动态离散化过程,使有限元模型自适应不同问题的求解策略。
3有限元分析的后i处理
后置处理主要对分析结果进行综合归纳,并进行可视化处理。从分析数据中提炼出设计者最关心的结果,检骏和校核产品设计的合理性。
主要包括:
(1)对应力和位移排序、求极值,检查应力和位移是否超出规定值.
(2)显示单元、节点的应力分布。
(3)动画模拟结构变形过程。
(4)应力、应变和位移的彩色浓淡图或等值线、等位面、剖切面、矢量图显示,绘制应力应变曲线等。
通过对大量分析数据所蕴含的工程含义进行判断推理,评价新产品工作性能与合理性,提出新产品设计方面的改进建议,使定量信息升华为深层次的定性信息。利用专家经验知识及时将分析的评价、改进意见映射为设计过程所能接受和处理的定量知识:(1)改变形状;(2)补充与完善形状;(3)改进结构件的支撑条件(如:增加/消除/重定位位移约束)}(4>改变外力;(5)改变材料;(6)调整约束极限,实现新产品的优化设计.
三、对连杆结构优化前后的有限元分析比较
1.连杆材料属性分析(略)
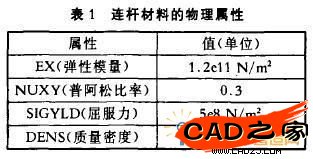
2.在Solidwork,中的有限元分析工具COSMOS指定零件的材料根据连杆的工作情况将表1的物理属性的合金钢材料指定给连杆,得出以下数据。

3.利用Solidwork:中的有限元分析工其COSMOS对改进前连杆进行分析
(1)载荷和约束信息

(2)应力及变形结果
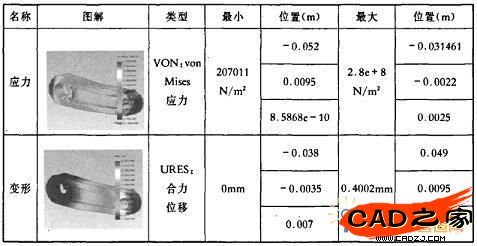
(3)分析结果
根据所指定参数,在连杆的分析及计算中找到的最低安全系数(FOS)为1.77113。
安全系数(FOS)是材料的屈服强度与实际应力的对比值.在SolidWork;中的有限元分析工具COSMOS中,使用最大等量应力标准来计算安全系数分布:当等量应力(von Mises应力)达到材料的屈服强度时,材料开始屈服,COSMOS中对某一点安全系数的计算是屈服强度除以该点的等量应力。
当某一位置安全系数小于1.0.表示该位置的材料已屈服,设计不安全。
当某一位置安全系数等于1.0,表示该位置的材料刚开始屈服。
当某一位置安全系数大于1.0,表示该位置的材料尚未屈服.
连杆的安全系数大于1.0,从前面对零件结构分析和简化的原则,以及从零件的工艺性角度考虑,有必要对连杆的结构作进一步的优化设计。
4.时结构优化设计后的连杆进行检查分析
在对零件结构在优化的过程中,主要是从零件的工艺性角度去除材料来考虑,连杆改变后的结构为,那么重要的一个环节就是在材料、载荷和约束信息不变的情况下,对其结构重新进行有限元分析和检查。应力及变形结果如下:
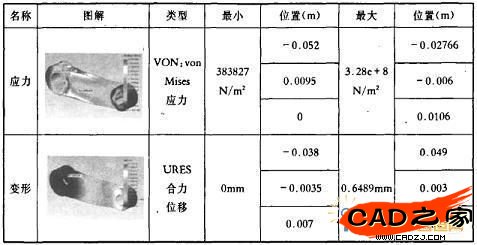
根据所指定参数,在连杆的分析及计算中找到的最低安全系数(FOS)为1.52,连杆的安全系数大于1.0,
四、有限元分析及结构优化结论
从分析结果来看,应力及变形情况结构改变前后变化不大,修改后的分析结果安全系数大于1.0,工艺性后者明显比前者要好的多,所以,连杆的优化设计是成功的。
在此次的结构设计过程中,有限元的分析、计算和检验对优化结果的肯定起了至关重要的决定性作用。
相关文章
- 2021-01-09AutoCAD 2010工程绘图及SolidWorks2010、UGNX7.0造型
- 2020-12-19AutoCAD 、SolidWorks实体仿真建模与应用解析 [芮勇勤
- 2013-08-22灰蓝色优雅三室两厅完整施工图+实景照片
- 2013-05-17发动机连杆的总成图、连杆体和连杆盖的零件图
- 2013-04-28北京优高雅吃通天沈阳万象城美食广场招标施工图
- 2011-03-10安稳优16m3石灰石粉螺旋秤
- 2011-03-10钢板仓内力与强度的有限元分析
- 2011-03-10带式输送机机架的有限元优化设计
- 2011-03-10带式输送机托辊间距优化设计
- 2011-03-10基于ADAMS的覆膜机输送机构优化设计