CAE软件操作技巧ABC

　　1 在ANSYS中如何显示梁截面

　　通过输入/eshape命令行即可.需要说明的是，一般的梁杆单元都可以通过/eshape命令显示截面，但是其截面均为根据输入的实常数所换算出的等效矩形截面，只有诸如beam44之类的单元可以保存通过Sections定义的截面形状并通过/eshape显示出来.

　　2 ANSYS中梁的铰接处理

　　通常，梁单元之间通过公用节点使得相邻的单元表现为固接形式，相当于在公用节点处约束全部自由度，而对于铰接的表现形式(约束平动自由度和释放转动自由度)，可以通过在铰接处建立2个keypoint，使得网格划分时在1点存在2个重合节点，而后在2个节点处通Preprocessor>Coupling Ceqn>Couple DOFS指定所有平动自由度相互耦合(释放了转动自由度)，这样即可模拟铰接.

　　3 ANSYS中梁问题的弯矩图绘制

　　在用ANSYS分析梁问题时，无法通General Postproc>Plot Results>Contour Plot查看弯矩结果，但可以通过定义etable实现.

　　首先需要明确想要查看的结果对应于所使用单元的编号(help中各单元信息的Item and Sequence Numbers表格)，然后在General Postproe>Eiement Table中定义相应的单元表，item为smisc，在箭头所示框内加入smisc中的项目编号.注意help中的石，Y，z方向为单元局部坐标.最后在General Postproc>Plot Results>Contour Plot>Line Element Res中分别选择I，J节点的elementtable，即可绘制弯矩图.

　　4 ANSYS梁问题截面方向定义

　　在分析梁问题时，有时需要定义梁截面的方向，可以在Preprocessor>Meshing>Mesh Attributes中定义，选择其中的Pick Orientation Keypoint(S)，点击确定后可以通过选择Keypoint定义网格划分后的截面方向.

　　5 使用完全积分单元时的剪力自锁问题及其解决方法

　　梁弯曲的基本特征见图1.当梁受弯时，轴向应变在厚度方向(竖直方向)上呈线性变化，厚度方向上无应变，也没有剪应变.如图2所示，1阶完全积分4节点四边形单元弯曲时，轴向应变通过积分点的水平长度变化，厚度方向应变通过积分点的垂直长度变化，而剪应变则是水平线与垂直线之间夹角的变化.单元中存在的剪应变与实际情况明显不符，这是由单元的数学描述而产生的.单元边不能弯曲使得原本不存在的剪应力出现，且使得单元变形表现为剪切变形而非弯曲变形，称为剪力自锁现象.

　　图1 梁弯曲基本特征

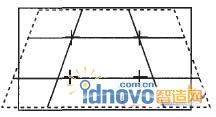
　　图2 完全积分单元剪力自锁

　　剪力自锁问题只影响受弯曲载荷的完全积分线性单元，这些单元功能在受直接或剪切载荷时没有问题.只有能确定在所分析的模型中载荷只会使结构产生小弯曲时，才可以采用完全积分线性单元.如果载荷产生的位移中包含较大的弯曲部分或不能确定其类型，则应该采用不同的单元类型.

　　由于2阶单元的边界可以弯曲(见图3)，没有剪力自锁问题，因此在分析一般问题时较接近理论值.但是，在复杂应力状态下，完全积分二次单元也可能发生锁死.此时需要采用其他的解决方法.

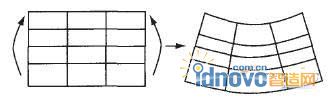
　　图3 受弯曲的完全积分二次单元的变形

    (1)使用减缩积分单元；

    (2)使用扩充节点的单元，例如原来使用4节点四边形单元，可改为8节点四边形单元；

    (3)单元形状尽可能规则，长宽比、斜度、锥度以及翘曲等都应得到控制以减少和避免自锁

6 使用减缩积分单元时的沙漏现象及其解决方法

    减缩积分单元与完全积分单元相比，在每个方向上少用1个积分点，因而1阶(线性)减缩积分单元只在单元中心有1个积分点．只有四边形和六面体单元才能采用减缩积分，而所有其他四面体和三角形采用完全积分，然而这2类单元可以同时使用．采用减缩积分单元可以解决剪力自锁问题，然而减缩积分单元在使用中又会产生沙漏问题．

    沙漏问题是指减缩积分单元在弯曲时出现如图4所示的形状类似沙漏的不正常应变，因而得名．这是因为单元在变形时，通过积分点的水平和垂直线长度以及两者夹角均没有变化，单元单个积分点上所有的应力分布都为0．由于单元扭曲产生应变能，所以这种弯曲的变形模态是零能量模式．在较粗的网格中，这种零能量模式可以通过网格扩展，从而产生无意义的结果．

图4 减缩积分单元的沙漏问题

    如果分析对象中有多个此类单元沿厚度方向排列，则分析对象的变形情况计算结果见图5．在厚度方向上可测得正确的轴向应变，剪应变为0．因此，只要低阶减缩积分单元足够精细(在厚度方向至少4个单元)，可以用此类单元模拟弯曲问题．

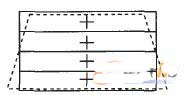
图5 低阶减缩积分单元模拟弯曲时变形情况的计算结果

    针对减缩积分单元沙漏问题的解决方法如下：

    (1)使用完全积分单元；

    (2)控制减缩积分单元的尺寸，只要单元足够精细，仍然可以保证准确度；

    (3)使用非协调单元．