加工中心几何误差的测量方法
时间:2011-05-30 08:39:30 来源:未知
1 引言
数控机床加工的高精度取决于多种因素,其中主要的因素之一是机床自身的运动精度。机床导轨的几何误差对运动精度影响甚大,使得刀具与被加工工件的相对位置发生改变,降低了加工精度。在机床几何误差测量的实践中,激光干涉仪是一种常用的测量仪器,配以适当的附件,即可进行线位移、角位移和直线度的测量。但在测量过程中,普通激光干涉仪经一次安装调整,仅能测量一项误差。同时,要获取按检定规程要求的全部几何误差,不仅要用到激光干涉仪,还要利用直角尺、自准仪、电子水平仪等(普通激光干涉仪不具备测量转角、垂直度等误差项的功能),所需的检测仪器、量具较多,安装调整费时,不能满足经济快速的测量要求。
针对以上问题,本文基于机床位移误差的建模与分析,提出了一种测量和辨识三坐标加工中心几何误差的方法,实际应用效果令人满意。
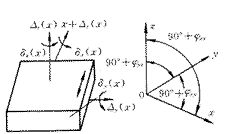
图1 机床运动副误差

1.主轴 2.刀具 3.工件 4.工作台 5.滑台 6.基座
图2 机床各运动部件坐标系示意图
2 位移误差模型的建立
当机床的滑台沿导轨移动时,假定导轨副作刚体运动。由于制造及安装误差的存在,运动有六个自由度,即运动轴向存在定位误差(线位移误差),在其余五个自由度也有微量误差(线位移或称直线度误差和角误差),故有六种运动可能影响滑台的最终位置。这样,机床的三个轴向运动共有18项误差,同时三轴之间还存在三项关系误差—垂直度误差Ø(Øxy,Øyz,Øxz)。一台三轴机床实际上共有21项原始误差(图1)。它们综合在一起,影响机床刀具与工件的最终相对位置。
假设机床各运动部件为刚体,角误差很小,为利用齐次变换描述运动部件相对于参考坐标系的位置,需确定参考坐标系和机床各运动部件的坐标系(图2)。设运动部件坐标系的X、Y、Z轴分别平行于机床标准坐标系的X、Y、Z轴。参考坐标系R的原点选择在机床固定基座上的某点;滑台A坐标系T4设定在Y向导轨上,工作台B坐标系TB设定在X向导轨上,主轴C坐标系TC设定在Z向导轨上,这三个坐标系的初始位置均与参考坐标系R重合。在参考坐标系原点处,机床系统误差均为零。
以对工作台B沿机床标准坐标系的X轴向运动进行测量为例,推导利用位移误差模型的表达式。首先,让滑台A回参考点,将反射镜安装在机床工作台面上,干涉仪装夹在主轴上,并将此位置记为对X轴进行标定的位置。当工作台B坐标系TB中的点(x,0,0)沿X轴向移动时,可测出工作台沿X轴向运动的位移误差Dx(x),以及Y向和Z向的直线度误差Dy(x)和Dz(x)。该点在参考坐标系中的位置为
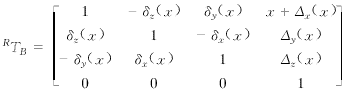
(1)
若测量系统的安装位置偏离了对X轴进行标定的位置,假设机床各部件为刚体,安装位置的偏移不影响转角误差的测量值,即转角误差只与该轴的坐标位置有关,不受其它轴坐标位置的影响。但在不同的测量位置上,位移误差的测量值不同,这是因为位移误差与转角误差和测量位置偏移量有关。
为寻求两个不同位置上的位移误差之间的关系,在工作台B坐标系T#p#分页标题#e#B中选择点b1(x1,y1,z1),在该点安装测量系统,x1,y1,z1为测量系统安装位置相对于进行机床标定位置的偏移值。以b1点为原点建立坐标系B1和B2,设B1为定坐标系,B2为动坐标系。在初始位置,B1和B2重合,且B1相对于参考坐标系R、工作台B的坐标系相对于B2的变换关系分别为
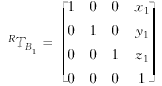
(2)
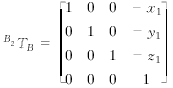
(3)
当点b1沿X轴向移动时,可测出X轴向运动的位移误差D′x(x),以及直线度误差D′y(x)、D′z(x)。此时,坐标系B2相对于坐标系B1的变换关系为下式
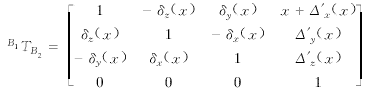
(4)
根据关系式(2)、(3)、(4),运用齐次变换法,可得
RTB= RTB1· B1TB2· B2TB
(5)
对上式右边进行连乘,并令方程两边对应项相等,有
Dx(x)=D′x(x)-dy(x)z1+dz(x)y1
(6)
Dy(x)=D′y(x)-dz(x)x1+dx(x)z1
(7)
Dz(x)=D′z(x)-dx(x)y1+dy(x)x1
(8)
D′x(x)=Dx(x)+dy(x)z1-dz(x)y1
(9)
D′y(x)=Dy(x)+dz(x)x1-dx(x)z1
(10)
D′z(x)=Dz(x)+dx(x)y1-dy(x)x1
(11)
此三式即为工作台位移误差模型。同理,可推导出滑台和主轴位移误差模型。
3 几何误差的九线测量法#p#分页标题#e#
测量工作台沿X轴向运动的几何误差时,在工作台B坐标系TB中选取(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)三点,使用激光干涉仪测量这三个点沿X轴向运动的线位移误差(图3中的线1、2、3)。由基本关系式(9)、(10)、(11)可知,对线1,测量X轴向运动的位移误差D′x1(x),以及Y向和Z向的直线度误差D′y1(x)与D′z1(x),有
D′x1(x)=Dx(x)+dy(x)z1-dz(x)y1
(12)
D′y1(x)=Dy(x)+dz(x)x1-dx(x)z1
(13)
D′z1(x)=Dz(x)+dx(x)y1-dy(x)x1
(14)
对线2,测量X轴向运动的位移误差D′x2(x),以及Y向的直线度误差D′y2(x),有
D′x2(x)=Dx(x)+dy(x)z2-dz(x)y2
(15)
D′y2(x)=Dy(x)+dz(x)x2-dx(x)z2
(16)
对线3,测量X轴向运动的位移误差D′x3(x),有
D′x3=Dx(x)+dy(x)z3-dz(x)y3
(17)
将以上六式联立,用矩阵表示为
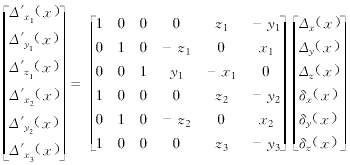
(18)
式(18)左边各项为测量值,只要在选取测量点时,保证等式右边的系数矩阵满秩,则上式有唯一解,可计算辨识出Dx(x)、Dy(x)、Dz(x)、dx(x)、dy(x)、dz(x)。
同理,可计算辨识Y轴向和Z轴向运动的的各误差项。由于要获取每一运动轴的六项几何误差需在三条线上进行测量,故对三轴加工中心而言,需在九条线上进行测量(图4)。
#p#分页标题#e#沿测量线1、4、7,对X、Y、Z轴的直线度误差进行测量后,利用各轴的直线度误差数据,可计算出三项垂直度误差Øxy、Øyz、Øxz。下面以计算Øxy为例,说明垂直度的计算方法。
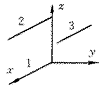
图3 用于测量x轴向运动误差的三条测量线
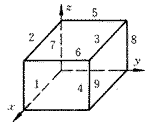 图4 九条测量线示意图
图4 九条测量线示意图
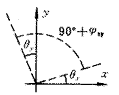
图5 x,y轴为机床标准坐标轴虚线为机床的实际轴线
若已知直线度Dy(x)与Dx(y)在各测点xi和yi处的数值,运用最小二乘法逼近Dy(xi)和Dx(yi),得到如图5所示的两条虚线,这两条虚线与标准坐标轴X、Y之间存在偏差角qx、qy,根据图5所示各角关系有
则
若Øxy>0,表示X、Y坐标轴之间的角度大于90°。同理,可求Øyz、Øxz。
4 实验与结论
实验在一台配备有华中Ⅰ型数控系统的XHK加工中心上进行,使用HP5528A双频激光干涉仪进行测量。这里以辨识X轴的偏摆角和俯仰角为例,说明九线测量法的实际运用。由于工作台在X轴向上的行程为750mm,选取位移误差的测量间隔为50mm,在每测量点上重复测量5次,并取平均值。
表1
测点序号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
D′x1(x)(µm)
0.0
1.1
-4.8
-1.8
-2.9
-2.0
-4.6
-1.3
-0.2
0.6
1.0
4.8
9.4
4.2
4.2
2.1
D′x#p#分页标题#e#2(x)(µm)
0.0
1.2
-4.7
-1.6
-2.6
-1.2
-3.7
-0.2
1.0
2.0
2.5
6.5
11.3
6.3
6.5
4.6
D′x3(x)(µm)
0.0
1.0
-5.2
-2.7
-4.1
-3.6
-6.5
-3.3
-2.3
-1.8
-1.9
1.8
6.1
0.5
0.1
-2.5
dy(x)(µm/m)
0.0
-0.8
-3.5
-7.7
-10.2
-13.1
-15.8
-16.5
-17.6
-20.2
-24.4
-25.4
-27.6
-30.5
-34.2
-38.1
dz(x)(µm/m)
0.0
1.0
-1.1
-2.3
-3.4
-8.5
-9.4
-10.7
-11.6
-14.3
-14.8
-16.6
-18.9
-21.3
-23.1
-25.2
表2
测点序号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
dy(x)(µm/m)
0.0
-1.9
-5.3
-8.5
-11.8
-14.4
-16.1
-17.3
-19.0
-22.3
-25.3
-27.1
-29.3
-32.3
-36.3
-40.5
dz(x)(µm/m)
0.0
2.4
-0.3
-3.5
-4.4
-7.3
-10.0
-12.5
-13.9
-16.0
-17.1
-19.4
-21.1
-23.4
-25.4
-27.0
#p#分页标题#e#
在坐标系TB中选取三个点b1(x1,0,78)、b2(x2,100,78)和b3(x3,0,198),当这三个点沿X轴向运动时,测得位移误差D′x1(x)、D′x2(x)、D′x3(x)。根据式(12)、(15)、(17),即可计算辨识出dy(x)和dz(x)。测量数据及dy(x)和dz(x)的计算辨识结果见表1。dy(x)和dz(x)的实测值见表2。由表1与表2的数值比较可知,利用本文所提出的九线法可以用于测量和辨识三坐标加工中心的全部21项几何误差。只要被测机床具有良好的稳定性和重复性,几何误差的辨识精度可以得到保证。实验表明,应用该方法进行测量,可显著减少所需测量仪器、量具、量仪的数量及安装调整时间,便于在工业现场使用。


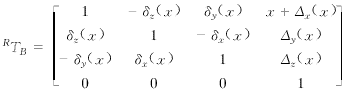
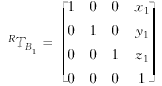
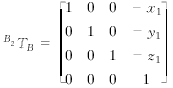
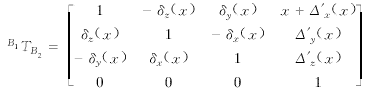
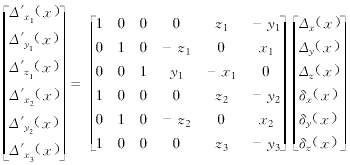

 图4 九条测量线示意图
图4 九条测量线示意图