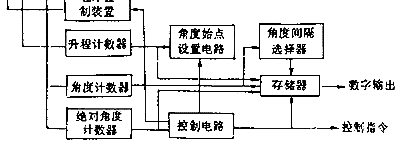
1 概述
2 凸轮轴应检测的内容
- 正确选择检测基准;
- 准确确定检测位置;
- 求解(测算)检测起始转角;
- 正确选择升程起始位置(基准),即“零升程”;
- 进行凸轮升程和基圆的圆跳动量检测;
- 对凸轮升程检测数据进行处理,求出符合“最小条件”要求的升程误差;
- 给出各凸轮的实际基圆半径;
- 按有关专业标准和升程公差要求,判定凸轮升程的合格性;
- 其它,如基准轴颈的直径,凸轮型面的表面粗糙度等;
- 对被检凸轮轴作出实用性结论。
3 检测基准选择
4 检测起始转角的求解与升程检测技巧
5 升程检测数据的处理
5 DEFDBLA-H
10 INPUT“输入所测点数及左点数:”,I,M
15 INPUT“输入左右侧升程上下偏差:”,ES1,EI1,ES2,EI2
20 INPUT“输入检测起始转角:”,AO
25 DIM A(I),B(I),C(I),H(I)
30 FOR S=1 TO I
35 INPUT“按顺序输入所测点转角值:”,A(S)
40 INPUT“按顺序输入所测点升程误差值:”,B(S)
45 INPUT“按顺序输入所测点升程变化率值:”,C(S)
50 NEXT S
55 D=B(1):E=B(1):F=B(1):G=B(1)
60 FOR J=1 TO M
65 IF D>B(J)THEN GOTO 75#p#分页标题#e#
70 D=B(J):N=J
75 IF E
90 NEXT J
100 FOR K=M+1 TO I
110 IF F>B(K) THEN GOTO 130
120 F=B(K):P=K
130 IF G
150 NEXT K
160 PRINT“左侧最大点:”,A(N),B(N),C(N)
165 PRINT“左侧最小点:”,A(O),B(O),C(O)
170 PRINT“右侧最大点:”,A(P),B(P),C(P)
175 PRINT“右侧最小点:” A(Q),B(Q),C(Q)
180 IF ABS(C(N))>ABS(C(O))AND ABS(C(P))>ABS(C(O)THEN: GOTO 210
190 IF ABS(C(N))>ABS(C(Q))AND ABS(C(P))>ABS(C(Q)THEN: GOTO 210
200 PRINT“应使两最小点等距”:L=0:IF B(N)>B(P) THEN PRINT“最大点为”,B(N)ELSE PRINT“最大点为”,B(P):GOTO 220
210 PRINT“应使两最大点等距”:L=1:IF B(O)>B(Q) THEN PRINT“最小点为”,B(Q)ELSE PRINT“最小点为:B(O)”
230 DD=3.1415926#/180
240 A1=A1*DD:A2+A2*DD:A3=A3*DD:A4=A4*DD
250 IF L=0 GOTO 270
260 A11=((ES1-ES2)-(B(N)-B(P)))/(C(N)-C(P))
265 A10=AO+A11:GOTO 280
270 A11+((EI1-EI2)-B(O)-B(Q)))/(C(O)-C(Q))
275 A10=AO+A11
280 PRINT“检测起始转角和转换量及起始转角优解值:”,AO,A11,A10
290 FOR T=1 TO I:H(T)=B(T)+C(T)*A11
300 以PRINT“转换前后升程误差值:”,A(T),H(T):NEXT T
310 D=H(1):E=H(1)
320 FOR T=1 TO I
330 IF D>H(T) THEN GOTO 350
340 D=H(T):M=T
350 IF E
370 NEXT T
380 H10=D-E
390 PRINT“最小包容区域宽度为:”,H10
400 PRINT“最大误差点转角及误差值:”,A(M),H(M)
410 PRINT“最小误差点转角及误差值:”,A(N),H(N)
420 END
6 升程合格性判定
相关文章
- 2021-09-08BIM技术丛书Revit软件应用系列Autodesk Revit族详解 [
- 2021-09-08全国专业技术人员计算机应用能力考试用书 AutoCAD2004
- 2021-09-08EXCEL在工作中的应用 制表、数据处理及宏应用PDF下载
- 2021-08-30从零开始AutoCAD 2014中文版机械制图基础培训教程 [李
- 2021-08-30从零开始AutoCAD 2014中文版建筑制图基础培训教程 [朱
- 2021-08-30电气CAD实例教程AutoCAD 2010中文版 [左昉 等编著] 20
- 2021-08-30电影风暴2:Maya影像实拍与三维合成攻略PDF下载
- 2021-08-30高等院校艺术设计案例教程中文版AutoCAD 建筑设计案例
- 2021-08-29环境艺术制图AutoCAD [徐幼光 编著] 2013年PDF下载
- 2021-08-29机械AutoCAD 项目教程 第3版 [缪希伟 主编] 2012年PDF
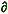 h/
h/