喷油嘴椭球面手工编程方法的实现

　　近年来，数控自动编程发展迅速，有很多以计算机图形学为基础的自动编程软件(如MasterCAM、UG等)，有效地解决了几何造型、零件几何形状的显示、交互式设计、修改以及刀具轨迹生成等问题，使得CAD/CAM逐步走向一体化。然而，数控自动编程必须增加计算机硬件和软件系统，增加了设备投资;自动编程软件的学习以及熟练运用需要一定的时间，需要一定的计算机知识和一定的机械基础知识，而且现代的编程软件为了做到功能全面，增加了许多新的加工概念和方式，软件包整体比较复杂和庞大，若想熟练掌握运用存在一定困难;自动编程产生的加工程序一般比较长，同样的零件，自动编程的程序可能是手工编程的程序长度的几倍甚至几十倍，其加工时间相应地会成倍或成几十倍地增长，这是其无法修正的根本缺陷。因此，对于小批量生产、形状相对简单的外冷喷油嘴的椭球面部分来说，采用手工编程，利用逼近圆的方法编写C语言程序，把椭球面用球面来近似，计算出若干个点，最终通过这些点编制外冷喷油嘴的椭球面部分的数控程序，加工形成椭球面轮廓的方法是可行的，既节约了成本，也节省了加工时间。

　　一、椭球面的逼近处理

　　对于喷油嘴的椭球面部分，数学处理的任务是用直线段或圆弧段去逼近非圆轮廓。喷油嘴的零件图如图1所示。

　　在车床上车削椭球面，车床系统只有直线插补和圆弧插补功能，没有椭圆曲线插补功能。因此，对于椭圆曲线的逼近也有两种方式。一是直线逼近：如果曲线方程比较简单，又不准备做理论误差验算，那么借助计算器就可以完成，但直线逼近的误差较大，只适用于比较粗糙的加工。另一种是用圆弧逼近。圆弧逼近一般应借助微机来完成，也有两种逼近方式。

　　一种方法是先按估计分段，编写一个程序作逼近，然后再编一个程序验算误差，如果算出的误差超过允许值，再回过来增加分段数，反复几次，直到误差略小于允许值为止。此法操作起来虽麻烦一些，但两个程序都比较简单。另一种方法是边逼近边计算误差，使算出的逼近圆弧与实际轮廓间的误差总是小于或等于某个允许值。

　　这样的程序虽然复杂一些，但机上操作就简单多了。图2所示的是喷油嘴的剖面图。

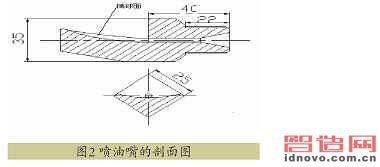
　　在喷油嘴椭球面部分的圆弧逼近中，本文选择等误差逼近方法，它能以最少的逼近圆

　　弧段来获得最高的逼近精度。如能把每段逼近圆弧与椭圆间的距离限制在1μm之内，那么由编程引起的理论误差就可以忽略不计了。编制如此精密逼近的数控加工程序，关键是作等误差逼近计算。只要算出每个逼近圆的数据，编写加工程序就很方便了。

　　1.方法的选择

　　对需要加工的那段椭圆作等分，如图3所示。在AB上沿逆时针方向取点，依次为U1，U2，…，Un。一种取法是让相邻两点间的x向距离相等，然后用椭圆方程算出各点的y值。这种取法的缺点是各区段弧长相差甚大，而且曲线段越长的区段的曲率变化越大。

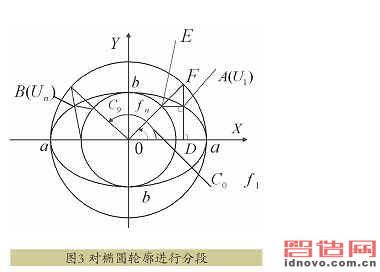
　　采用另外一种取法，即让相邻两点的参数值相等。椭圆的参数方程如式(1)所示。

　　看一下变量中的几何意义。先以a、b为半径作两个同心圆，再作半径OF，交于点E。从F点作X轴的垂线FD，再从 E点作X轴的平行线，并与FD交于A。把∠FOX作为变量，用Ф表示。把点 A确定在加工起点，并用U1(x1，y1)表示，令其相应的参数角为Ф1。给参数一个增量Δ Ф，令Ф1+ΔФ=Ф2，与Ф2相应的点用U2(x2，y2)表示，那么用此法沿逆时针依次取U3，U4，…，Un，Un应到达或略超过加工终点B，这种用相同参数增量取的点群，其相邻两点间的弧长相差不大。

　　2.逼近圆的一般概念和计算

　　在上述椭圆上任取两点P(x1，y1)、Q(x3，y3)，它们的参数角分别为C1、C3;在椭圆轮廓的PQ间取一点M2(x2，y2)，使其对应的参数C2=(C1+C3)/2。令PM2、M2Q的中点分别为M4(x4，y4)和M5(x5，y5)。从M4、M5分别作PM2、M2Q的垂线，这两条垂线交于O(x0，y0)，O就是P、M2、Q三点决定的圆的圆心，亦即与PQ间椭圆曲线逼近的圆的圆心，OP是圆的半径。根据已知条件来计算这个逼近圆。如图4所示，直线OM4和OM5的方程联立，解得这个圆的方程如式(2)所示。

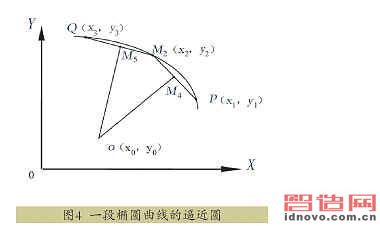
　　3.逼近圆误差的一般计算

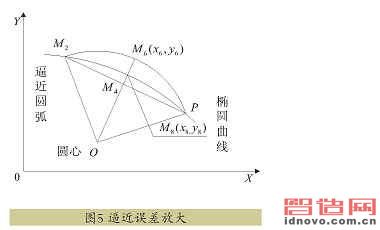
　　把图4的右半部分放大，作成图5。令 OM4的延长线与圆的交点为M6(x6，y6)、与椭圆的交点为M8(x8，y8)。可以把M6M8的长度看作是这部分的最大误差。为求M6M8的长度，先得计算M6、M8点的坐标值。M6的坐标是直线方程OM4和圆方程(2)组成的方程组的解。M8的坐标是由直线方程OM6和椭圆方程组成的方程组的解，式中的正负选择与x4的正负号相同后，经过计算M6M8的长度为

　　将右侧PM2间的最大误差D1与允许误差作比较，判别是否超差。再用同样的方法算出左侧M2Q间的最大误差D2，将它与允差作比较，判别是否超差。只有左右两部分均未超差才能认定截取的PQ间没有超差。

　　4.实用逼近圆的选择

　　如图3所示，先把第1、3点U1、U3分别作为P、Q点，即取P=1、Q=3。按上述方法作第一个逼近圆的计算、误差计算和判别。如未超差，就改取U1、U4作为P、Q点，即取P=1、Q=4作第二个圆，再进行相应的计算和判别。只要不超差，圆就继续试作下去。如作到第W个圆算出超差，那么前一个圆，即过P=1、Q=W-1点的圆，就是找到的第一个实用逼近圆。这个实用逼近圆Q点的坐标、圆心相对于P点的X、Y向距离I、J和圆半径，都是有用的数据。

　　接着找第二个实用逼近圆。将第一个实用逼近圆弧的终点 Q，即(Q=W-1)作为新的P点，紧接着的下一个点作为新的Q点，重新开始作第一个圆，经计算如不超差，就将Q再往前取一点，作第二个圆，直到作到第L个圆算出超差，那么前一个圆( L-1)就是找到的第二个实用逼近圆。这样依次找下去，直到某个实用逼近圆弧的终点达到或超过椭圆的加工终点B为止，找到若干个实用逼近圆。

　　二、C语言程序的编写

　　每个参数角增量取0.00063弧度比较适当，这意味着整个圆要分成近万段。这就要计算近万个圆和近两万个误差，显然这必须借助计算机来实现。根据以上的计算方法和思路，编制了C语言程序，部分程序如下.

　　#include

　　#include

　　main()

　　{

　　double x,y,x0,y0,

　　…

　　..,a,b,r,d1,d2;定义各个参数。

　　Int q;

　　c0=3*1.570796;初始点参数角值。

　　c1=c0;

　　c3=c0+q*0.00063;

　　c2=(c1+c3)/2;

　　x1=a*cos(c1);

　　y1=b*sin(c1);

　　x3=a*cos(c3);

　　y3=b*sin(c3);

　　……

　　scanf("%f,%f,%f”,&a,&b,&q);输入椭圆的长轴，短轴以及点数

　　printf("%f,%f,%f,%f,%f",a,bx, y,r,d1,d2);输出逼近圆x，y的坐标值以及圆的半径，

　　d1，d2为是否超差，如超差，该值舍去

　　}

　　三、数控程序的编制及加工过程的实现

　　该零件在CAK6150DI卧式数控车床上加工，该机床采用FANUC数控系统，这里需要注意一点，用C语言程序计算出来的x、y、r等值需要转换成机床上的加工代码，x值即是机床的z向坐标值，y值的2倍就是数控程序x轴的坐标值。编制的部分数控程序代码如下。

　　粗车部分程序：

　　G00 x52.34,z45.0;

　　G03 x59.23,z44.86,

　　R58.53,F0.15;

　　G03 x65.56,z38.01,

　　R68.61,F0.15;

　　G03 x71.09,z29.74,

　　R79.12,F0.15;

　　G03 x75.41,z19.55,

　　R89.06,F0.15;

　　G03 x77.58,z6.2,R96.66,F0.15;

　　…

　　精车部分程序：

　　…

　　G03 x59.60,z45.0,R58.91,F0.08;

　　G03 x65.95,z38.10, R69.03,F0.08;

　　G03 x71.47,z29.83, R79.55,F0.08;

　　G03 x75.80,z19.63, R89.49,F0.08;

　　G03 x78.0,z5.0, R97. 10,F0.08;

　　G01 x36.5z5.0, F0.08;

　　G00x36.5z50.0;

　　T0100;

　　M05;

　　M30;

　　四、结束语

　　数控手工编程在任何时候都是必要的，是编程技术不可缺少的一部分。中等难度以下零件的手工编程的难点多在于数值点的计算和处理，而且手工编程并不排斥计算机的应用，通用软件在辅助人工计算处理图形节点、坐标数值点方面极为有效。通常进行人工计算需要花费半天甚至一天的图形，利用编写程序，在计算机上仅用十多分钟就能完成数值计算，而且能保证一定的精度。所以根据逼近圆的方法，利用计算机辅助，最终通过数控编程实现了椭球面的加工。

　　实践证明，这种方法是可行的，不仅节约了成本，而且节省了加工时间。