[摘要] 预应力索杆体系在点支式玻璃建筑支承结构中得到了广泛的应用,但对这类体系的原理和特性的认识还很不充分,目前所采用的方法和工具,有些还不能完全反映结构的真实情况。本文在考虑索杆结构几何非线性影响的基础上,利用通用有限元软件ANSYS 的非线性模块,对索杆体系初始预应力状态和工作状态下的结构受力性能进行了深入分析。分析结果表明,利用ANSYS 可以很方便地解决索杆体系的非线性分析问题。
关键词 索杆结构 非线性原理 有限元分析
1 引言
点支式玻璃幕墙索杆支承体系主要由拉杆(索)式结构组成,即采用不锈钢拉杆或用与玻璃分缝相对应的钢拉索代替一般的钢构件,形成幕墙的支承结构,玻璃通过金属连接件与其固定。通过给拉杆或拉索施加预拉应力,使其在各种可变荷载作用下都处于受拉状态,从而达到用柔性拉杆代替支承结构中的刚性构件的目的,避免了构件受压易失稳的问题,这样就可以采用截面较小的高强度钢构件,精致细巧,大大提高了建筑的通透性。
我国近年来在多项工程中采用了点支式玻璃幕墙技术,如深圳机场新航站楼、北京远洋大厦、北京植物园展览温室、南京国际会展中心和广州新白云机场航站楼等多项大型公共工程均采用了点支玻璃幕墙。但该种结构形式在国内的研究和应用总体上还处于起步阶段。
预应力索杆支承体系在点支式玻璃建筑中已经得到了大量的、广泛的应用。同工程应用相比,理论和试验方面的研究相对滞后。对这类体系的工作原理和结构特性还缺乏充分的认识,在实际工程的分析和计算中所采用的方法和计算工具有些还不能完全反映结构的真实情况。为使索杆支承结构能更加广泛地在点支式玻璃建筑中的应用,需要对其承载性能进行深入的研究,同时对其计算工具和方法的合理性、有效性进行分析论证,从而提出切实合理且便于工程应用的计算方法。
索杆支承结构依靠自平衡预应力维持结构的稳定,在没有形成预应力之前,结构是处于不稳定的机构状态,这是索杆结构区别于传统结构的本质特征。在预应力索杆支承结构中,结构刚度贡献主要来自于初始状态预应力。如果不考虑预应力的贡献,初始状态的结构刚度往往是奇异的,这就决定了这类结构体系的分析计算必须采用考虑应力刚度矩阵的非线性索杆有限元方法[2]。
索杆支承结构的整体刚度由预应力提供的刚度和截面刚度构成。索杆体系设计包括初始状态设计和工作状态设计两部分。初始状态是指索杆在预应力作用下的自平衡状态;工作状态是指索杆在组合外荷载作用下的平衡状态。索杆体系的初始状态应满足:初始状态是平衡的、稳定的,即应估算出索(杆)所需的最小张力,以保证工作全过程中索始终处于张紧状态。索杆体系的工作状态应满足:索杆体系的整体稳定、节点位移应满足要求;索杆体系中的拉索(杆)不宜应受压而退出工作,必须防止应拉索(杆)退出工作而使体系成为几何可变机构。即应考虑在对称和不对称风荷载作用下,能满足挠度限制和索杆结构强度、稳定所需的拉索(杆)中张力。
本文在利用通用有限元分析软件ANSYS 的非线性模块,结合有限元软件的功能和选用的索单元特点,对索杆体系初始预应力状态和工作状态进行了分析。总结了ANSYS 的有限元分析结果,研究了索杆体系荷载-位移全过程的结构性能,并对计算方法进行了分析。
2 有限元分析模型
随着计算机技术、固体力学和数值分析科学的飞速发展,有限单元法已成为工程数值分析的强大工具,尤其在固体力学和结构分析的领域内,有限元法取得了巨大的进展,许多通用程序和专用程序投入实际应用,利用这些程序成功地解决了一大批有重大意义的问题。
非线性问题包括状态非线性、材料非线性和几何非线性等。如果结构承受大变形,它变化的几何形状可能会引起结构的非线性相应,这就是结构的几何非线性问题。
索杆支承结构是典型的几何非线性大变形柔性结构。在该体系中,拉索属于柔性结构,具有大位移、小应变的变形特征,虽然构件的应变仍在材料的弹性范围内,应力、应交关系遵从虎克定律,但描述其变形特征的基本关系-应力与位移的关系是非线性的,其中非线性项的数值不像小变形问题那样相对线性项可以略去,而是不可忽略和必须考虑的量。基本关系的非线性使得所建立的力学微分方程成为非线性微分方程[4]。#p#分页标题#e#
索杆结构同时表现出一种与状态相关的非线性行为,例如,一根只能拉伸的钢索可能是松散的,也可能是绷紧的。相应的结构系统的刚度由于系统状态的变化而改变,亦即结构的面外刚度可能大大地受结构面内应力状态的影响。这种面内应力与横向刚度之间的耦合,通称为应力刚化。在薄的、高应力的结构中,如缆索或薄膜中,应力刚化现象是相当明显的。
一个鼓面,当它绷紧时会产生垂向刚度,这就是应力刚化的典型例子。尽管应力刚化理论假定单元的转动和应变是小的,然而在某些结构的系统中,应力刚化效应只能通过考虑几何非线性的影响来求得。
在有限元分析中,几何非线性通常包括初始应力效应,它作为几何非线性理论的一个子集,对于大多数实体和壳体单元,当大变形效应被激活时,将自动包括初始应力刚化效应。
为更全面研究索杆结构的承载性能,本文所涉及的几何非线性分析同时了考虑应力刚化效应的影响。
本文选择目前广泛采用的索杆支承体系的结构类型,进行其初始预应力状态和工作状态下承载性能的计算和分析,根据实际工程的几何和荷载参数,建立索杆支承结构的有限元分析模型,进行计算分析。
本文的有限元分析,采用ANSYS 中适用于几何非线性问题分析的杆单元。在分析中,常用的单元类型为Link8 单元和Link10 单元。Link8 单元只承受轴向力,不承受弯矩和剪力,且具有塑性、蠕变、膨胀、应力刚化、大变形、大应变、单元死活等功能。在索杆结构分析中,Link8 单元用来模拟其中的刚性杆。
Link10 单元独一无二的双线性刚度矩阵特性,使其成为一个轴向仅受拉或仅受压的单元。使用只承受拉力选项时,如果单元受压,刚度就消失,以此来模拟拉索的松弛。本单元不承受弯矩和剪力,只能轴向承受拉力或压力。本单元具有应力刚化、大变形、大应变等功能。在索杆结构分析中,Link10 单元用来模拟其中的拉索(杆)[5]。
由于索杆支承结构工作在弹性阶段,因此有限元分析时,可以不考虑结构材料的非线性,仅考虑几何非线性的影响。有限元分析时,假定材料为各向同性,钢材的弹性模量E 值按如下采用:普通碳素钢取2.02×105MPa;不锈钢和高强碳素钢为(1.8~2.0)×105MPa,高强钢丝和钢绞线取1.5×105MPa,泊松比取0.3。
根据国家标准《建筑结构荷载规范》(GB50009-2001)和《点支式玻璃幕墙工程技术规程》(CECS:127-2001)的规定,作用在点支式玻璃幕墙支承结构上的荷载和作用主要有凤荷载和地震作用。
作用在点支式玻璃幕墙中支承结构的风荷载标准值应按下式计算[2.3]:
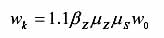
对于竖向的玻璃幕墙,垂直于玻璃平面的分布水平地震作用标准值可按下式计算[2.3]:
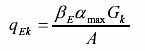
某国际会展中心点支式玻璃幕墙的竖向为主受力杆件方向,每6.75m 设有一榀钢管桁架,承担横向次受力构件传来的水平力。横向为次受力构件方向,每1.6m 设一榀拉杆桁架,承担三块玻璃面板传来的水平力,拉杆采用不锈钢棒,规格为?16,压杆也为不锈钢棒,规格为?40。设计简图和拉、压杆件初选截面如图1 所示。经计算,考虑凤荷载与地震作用组合下的桁架节点集中力为:标准值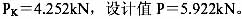
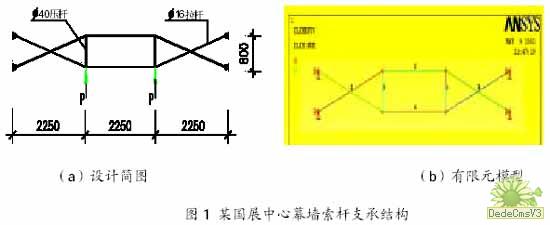
根据图1(a)所示的结构设计简图,利用ANSYS 建立的有限元计算模型如图1(b)所示,其中?16 拉杆采用Link10 单元,?40 压杆采用Link8 单元。
3 几何非线性分析
首先进行索杆支承结构初始预应力分布分析。
假定拉杆预应力初始值,相应的初始应变为,将其作为索单元的实常数输入,进而得到索杆体系的预应力分布如图2 所示。
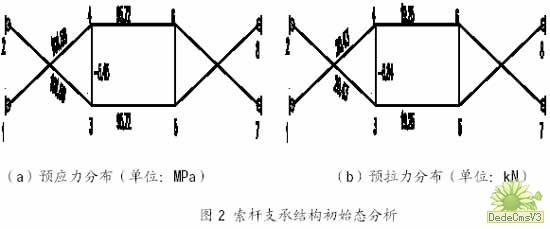
索杆支承结构初始态预应力分布的分析,是索杆结构承载性能分析的基础。在初始态分析阶段假定的索杆截面、预应力分布,能否满足在工作荷载下结构强度、稳定和刚度的要求,还有待工作状态计算结果的验证。#p#分页标题#e#
对具有预拉力的索杆结构体系在图1(a)所示水平荷载作用下,进行结构的非线性有限元分析。荷载设计值作用下的应力(内力)计算结果见图3 所示。
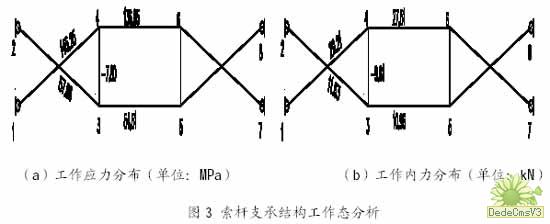
计算结果表明,在荷载标准值 作用下结点最大位移为1.58mm;在荷载设计值
作用下结点最大位移为1.58mm;在荷载设计值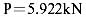 作用下,拉杆最大拉应力为145.25MPa,相应最大拉力为29.21kN,最小拉力为10.96kN。即结构拉杆的最大、最小拉应力及结构的最大位移为:
作用下,拉杆最大拉应力为145.25MPa,相应最大拉力为29.21kN,最小拉力为10.96kN。即结构拉杆的最大、最小拉应力及结构的最大位移为:

以上计算结果表明,在工作荷载作用下,索杆结构强度、刚度满足规范要求。
4 结论
计算结果表明,采用国际著名通用有限元分析软件确定预应力索杆体系的初始状态和工作状态,分析计算方便快捷,计算结果准确可靠,符合工程实际情况,证明所采用的计算方法是合理和可行的。
关键词 索杆结构 非线性原理 有限元分析
1 引言
点支式玻璃幕墙索杆支承体系主要由拉杆(索)式结构组成,即采用不锈钢拉杆或用与玻璃分缝相对应的钢拉索代替一般的钢构件,形成幕墙的支承结构,玻璃通过金属连接件与其固定。通过给拉杆或拉索施加预拉应力,使其在各种可变荷载作用下都处于受拉状态,从而达到用柔性拉杆代替支承结构中的刚性构件的目的,避免了构件受压易失稳的问题,这样就可以采用截面较小的高强度钢构件,精致细巧,大大提高了建筑的通透性。
我国近年来在多项工程中采用了点支式玻璃幕墙技术,如深圳机场新航站楼、北京远洋大厦、北京植物园展览温室、南京国际会展中心和广州新白云机场航站楼等多项大型公共工程均采用了点支玻璃幕墙。但该种结构形式在国内的研究和应用总体上还处于起步阶段。
预应力索杆支承体系在点支式玻璃建筑中已经得到了大量的、广泛的应用。同工程应用相比,理论和试验方面的研究相对滞后。对这类体系的工作原理和结构特性还缺乏充分的认识,在实际工程的分析和计算中所采用的方法和计算工具有些还不能完全反映结构的真实情况。为使索杆支承结构能更加广泛地在点支式玻璃建筑中的应用,需要对其承载性能进行深入的研究,同时对其计算工具和方法的合理性、有效性进行分析论证,从而提出切实合理且便于工程应用的计算方法。
索杆支承结构依靠自平衡预应力维持结构的稳定,在没有形成预应力之前,结构是处于不稳定的机构状态,这是索杆结构区别于传统结构的本质特征。在预应力索杆支承结构中,结构刚度贡献主要来自于初始状态预应力。如果不考虑预应力的贡献,初始状态的结构刚度往往是奇异的,这就决定了这类结构体系的分析计算必须采用考虑应力刚度矩阵的非线性索杆有限元方法[2]。
索杆支承结构的整体刚度由预应力提供的刚度和截面刚度构成。索杆体系设计包括初始状态设计和工作状态设计两部分。初始状态是指索杆在预应力作用下的自平衡状态;工作状态是指索杆在组合外荷载作用下的平衡状态。索杆体系的初始状态应满足:初始状态是平衡的、稳定的,即应估算出索(杆)所需的最小张力,以保证工作全过程中索始终处于张紧状态。索杆体系的工作状态应满足:索杆体系的整体稳定、节点位移应满足要求;索杆体系中的拉索(杆)不宜应受压而退出工作,必须防止应拉索(杆)退出工作而使体系成为几何可变机构。即应考虑在对称和不对称风荷载作用下,能满足挠度限制和索杆结构强度、稳定所需的拉索(杆)中张力。
本文在利用通用有限元分析软件ANSYS 的非线性模块,结合有限元软件的功能和选用的索单元特点,对索杆体系初始预应力状态和工作状态进行了分析。总结了ANSYS 的有限元分析结果,研究了索杆体系荷载-位移全过程的结构性能,并对计算方法进行了分析。
2 有限元分析模型
随着计算机技术、固体力学和数值分析科学的飞速发展,有限单元法已成为工程数值分析的强大工具,尤其在固体力学和结构分析的领域内,有限元法取得了巨大的进展,许多通用程序和专用程序投入实际应用,利用这些程序成功地解决了一大批有重大意义的问题。
非线性问题包括状态非线性、材料非线性和几何非线性等。如果结构承受大变形,它变化的几何形状可能会引起结构的非线性相应,这就是结构的几何非线性问题。
索杆支承结构是典型的几何非线性大变形柔性结构。在该体系中,拉索属于柔性结构,具有大位移、小应变的变形特征,虽然构件的应变仍在材料的弹性范围内,应力、应交关系遵从虎克定律,但描述其变形特征的基本关系-应力与位移的关系是非线性的,其中非线性项的数值不像小变形问题那样相对线性项可以略去,而是不可忽略和必须考虑的量。基本关系的非线性使得所建立的力学微分方程成为非线性微分方程[4]。#p#分页标题#e#
索杆结构同时表现出一种与状态相关的非线性行为,例如,一根只能拉伸的钢索可能是松散的,也可能是绷紧的。相应的结构系统的刚度由于系统状态的变化而改变,亦即结构的面外刚度可能大大地受结构面内应力状态的影响。这种面内应力与横向刚度之间的耦合,通称为应力刚化。在薄的、高应力的结构中,如缆索或薄膜中,应力刚化现象是相当明显的。
一个鼓面,当它绷紧时会产生垂向刚度,这就是应力刚化的典型例子。尽管应力刚化理论假定单元的转动和应变是小的,然而在某些结构的系统中,应力刚化效应只能通过考虑几何非线性的影响来求得。
在有限元分析中,几何非线性通常包括初始应力效应,它作为几何非线性理论的一个子集,对于大多数实体和壳体单元,当大变形效应被激活时,将自动包括初始应力刚化效应。
为更全面研究索杆结构的承载性能,本文所涉及的几何非线性分析同时了考虑应力刚化效应的影响。
本文选择目前广泛采用的索杆支承体系的结构类型,进行其初始预应力状态和工作状态下承载性能的计算和分析,根据实际工程的几何和荷载参数,建立索杆支承结构的有限元分析模型,进行计算分析。
本文的有限元分析,采用ANSYS 中适用于几何非线性问题分析的杆单元。在分析中,常用的单元类型为Link8 单元和Link10 单元。Link8 单元只承受轴向力,不承受弯矩和剪力,且具有塑性、蠕变、膨胀、应力刚化、大变形、大应变、单元死活等功能。在索杆结构分析中,Link8 单元用来模拟其中的刚性杆。
Link10 单元独一无二的双线性刚度矩阵特性,使其成为一个轴向仅受拉或仅受压的单元。使用只承受拉力选项时,如果单元受压,刚度就消失,以此来模拟拉索的松弛。本单元不承受弯矩和剪力,只能轴向承受拉力或压力。本单元具有应力刚化、大变形、大应变等功能。在索杆结构分析中,Link10 单元用来模拟其中的拉索(杆)[5]。
由于索杆支承结构工作在弹性阶段,因此有限元分析时,可以不考虑结构材料的非线性,仅考虑几何非线性的影响。有限元分析时,假定材料为各向同性,钢材的弹性模量E 值按如下采用:普通碳素钢取2.02×105MPa;不锈钢和高强碳素钢为(1.8~2.0)×105MPa,高强钢丝和钢绞线取1.5×105MPa,泊松比取0.3。
根据国家标准《建筑结构荷载规范》(GB50009-2001)和《点支式玻璃幕墙工程技术规程》(CECS:127-2001)的规定,作用在点支式玻璃幕墙支承结构上的荷载和作用主要有凤荷载和地震作用。
作用在点支式玻璃幕墙中支承结构的风荷载标准值应按下式计算[2.3]:
对于竖向的玻璃幕墙,垂直于玻璃平面的分布水平地震作用标准值可按下式计算[2.3]:
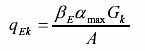
某国际会展中心点支式玻璃幕墙的竖向为主受力杆件方向,每6.75m 设有一榀钢管桁架,承担横向次受力构件传来的水平力。横向为次受力构件方向,每1.6m 设一榀拉杆桁架,承担三块玻璃面板传来的水平力,拉杆采用不锈钢棒,规格为?16,压杆也为不锈钢棒,规格为?40。设计简图和拉、压杆件初选截面如图1 所示。经计算,考虑凤荷载与地震作用组合下的桁架节点集中力为:标准值

根据图1(a)所示的结构设计简图,利用ANSYS 建立的有限元计算模型如图1(b)所示,其中?16 拉杆采用Link10 单元,?40 压杆采用Link8 单元。
3 几何非线性分析
首先进行索杆支承结构初始预应力分布分析。
假定拉杆预应力初始值,相应的初始应变为,将其作为索单元的实常数输入,进而得到索杆体系的预应力分布如图2 所示。

索杆支承结构初始态预应力分布的分析,是索杆结构承载性能分析的基础。在初始态分析阶段假定的索杆截面、预应力分布,能否满足在工作荷载下结构强度、稳定和刚度的要求,还有待工作状态计算结果的验证。#p#分页标题#e#
对具有预拉力的索杆结构体系在图1(a)所示水平荷载作用下,进行结构的非线性有限元分析。荷载设计值作用下的应力(内力)计算结果见图3 所示。

计算结果表明,在荷载标准值

以上计算结果表明,在工作荷载作用下,索杆结构强度、刚度满足规范要求。
4 结论
计算结果表明,采用国际著名通用有限元分析软件确定预应力索杆体系的初始状态和工作状态,分析计算方便快捷,计算结果准确可靠,符合工程实际情况,证明所采用的计算方法是合理和可行的。
相关文章
- 2021-09-08全国专业技术人员计算机应用能力考试用书 AutoCAD2004
- 2021-08-28计算机辅助设计与制造 21世纪全国应用型本科大机械系
- 2021-08-28计算机辅助设计与制造(CAD∕CAM)PDF下载
- 2021-08-27计算机辅助设计与制造 21世纪全国应用型本科大机械系
- 2021-08-27计算机辅助设计与制造(CAD∕CAM)PDF下载
- 2021-08-14新编AutoCAD 2004中文版计算机辅助设计应用技能培训教
- 2021-08-13中文AutoCAD 2008计算机辅助设计实训教程PDF下载
- 2021-08-03Autodesk RevitStructure2012应用宝典 [欧特克软件(中
- 2021-08-02Autodesk RevitMEP2012应用宝典 [欧特克软件(中国)有限
- 2021-08-02Autodesk Revit2013族达人速成 [欧特克软件(中国)有限公