3.2 水平向试验传感器受力情况分析
在传感器的指标中,倾覆力矩量程(Mx,My)为2600Nm,扭转力矩量程(Mz)为1550Nm。如果试验中卫星造成的倾覆力矩由8个传感器平均承担,则仅能测量2600×8=20.8KNm的倾覆力矩,这对于一般卫星试验来说显然是不够的。此外根据传感器的指标计算水平向测力可达8×60=480KN,水平向量程是否真有如此大?根据2.3节末尾的推论,FMD夹具的水平向受力情况远较垂直向来得复杂,以上两个结论到底是否正确还有待进一步验证,因此很有必要针对水平向试验的传感器受力情况进行详细分析。
由上文可知卫星质量2.7吨,质心高度1.65m,原夹具质量378Kg,试验水平向最大推力10吨,FMD夹具质量598.54Kg,试验最大量级1g。振动台推力公式如下:
F=kMA (1)
式中F为推力,k为有效质量系数,M为运动部件总质量,A为加速度。在纯加速度控制中,水平向卫星与振动台总的运动质量M=动圈(116Kg)+驱动块(50Kg)+滑板(347Kg)+附加铝板(500Kg)+夹具(378Kg)+卫星(2700Kg)=4091Kg,A=1×10=10m/s2,F=100KN,将M、A、F代入式(1),可得此卫星有效质量系数k=2.44。
在力限控制中,水平向卫星与振动台总的运动质量M=动圈(116Kg)+驱动块(50Kg)+滑板(347Kg)+附加铝板(500Kg)+夹具(598.54Kg)+卫星(2700Kg)=4312Kg,A=10m/s2,k=2.44,同样将M、A、k代入式(1),可得此卫星在力限试验中的预测最大推力为10.5吨。考虑到安全余量,将此推力放大20%,即12.6吨(126KN)作为静力分析的载荷,运用cosmos软件对FMD夹具进行静力计算。
在静力计算中约束下夹具各安装孔的3个平动自由度,载荷施加在上夹具顶部平面中心上方1.65m处,采用远程载荷多点刚性约束将载荷传递给上夹具与卫星连接的各个安装孔,传感器与上下夹具的8个螺钉连接采用刚性接头单元进行连接,以便传递力。约束状态见图10。
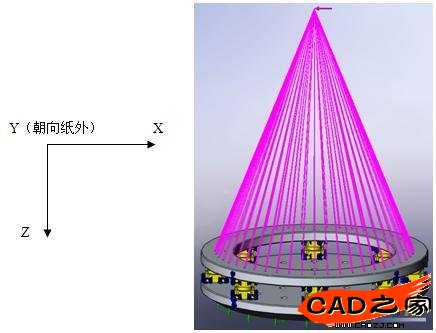
图10:静力计算约束状态
在分析中,分别计算各传感器与上夹具4个连接孔的三个方向的力以及其相对传感器顶面中心的力矩,然后再算出各传感器的三向合力及合力矩,经计算正交和斜交各传感器受力情况见表3,传感器序号见图4,5。
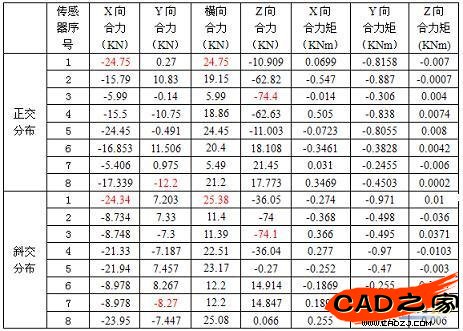
表3:传感器受力情况
由表3可知,正交分布最大X向合力为24.75KN,最大Y向合力为12.2KN,最大Z向合力为74.4KN,斜交分布最大X向合力为24.34KN,最大Y向合力为8.27KN,最大Z向合力为74.1KN,由此可见无论正交还是斜交其三个方向的合力都没有超过传感器的量程,而力矩方面都处在1KNm以下,完全不存在上述无法承担倾覆力矩的问题,能够满足试验测量的要求。此外从X向受力情况来看8个传感器的受力都不相同,当其中X向受力最大的传感器达到指标中的60KN时,其他的传感器还远没有达到60KN,因此其量程要远低于上述的480KN。
表3中的Z向合力可用于倾覆力矩的测算,其中两种分布情况受拉向的力都远大于受压向的力,这种现象根据材料力学弯矩原理说明在水平向试验中倾覆力矩中心并不处于夹具的中心,而是靠近受压端,且在真实试验中该中心呈正弦方式相对夹具中心来回摆动,并随着推力的变化其摆动幅度也将随之改变。
3.3 螺钉校核
根据以往试验的经验,水平向由于倾覆力矩的参与,螺钉在垂直向无论最大轴向应力还是最大横向应力都小于水平向,且传感器与夹具连接的方式为一端通孔、一端螺纹孔,通孔直径略大于螺钉外径,形成间隙配合,这种连接方式仅能看作普通螺栓连接而不能看作绞制孔连接。因此根据机械设计手册关于普通螺栓连接的应力校核方法,本节将着重针对传感器与上夹具连接螺钉进行轴向应力和横向应力两个方面的校核,并通过预紧力计算出螺钉的最小扭矩,最后根据扭矩校核其剪切应力。
从表3可以看出最大横向力为25.38KN,最大轴向力为74.4KN,由于两种分布方式横向和轴向最大合力区别不大,因此仅以这两个最大的数据作为校核的载荷条件。
3.3.1 轴向应力
传感器与上夹具连接螺钉为4个碳钢8.8级M16 2.0螺钉,传感器顶部平面相对于整个FMD夹具来说可简化为一点,4个螺钉的受力误差忽略不计,因此认为传感器的最大轴向力由4个螺钉均分承担,每个螺钉承受的最大轴向力F=74.4/4=18.6KN。校核螺钉轴向应力公式如下:
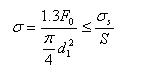 (2)
(2)
式中 为螺钉轴向应力;S为最大应力安全系数,在控制预紧力的情况下,S应取1.2~1.5,在此为了安全取1.5;d1为螺钉小径,查表得M16 2.0螺钉小径为13.835mm; 为螺钉的屈服极限,查表得8.8级碳钢螺钉屈服极限为640MPa;F0为螺钉总拉力,它是螺钉所受轴向载荷与剩余预紧力之和见下式:
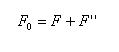 (3)
(3)
式中F"为剩余预紧力,查表得在承受动载荷的情况下其值应取(0.6~1.0)F,为了安全取1.0F,由此可得F0=2F=2 18.6=37.2KN。将S、F0、d1代入式(2)得 =321.7MPa<640/1.5=426.7MPa,轴向应力符合安全要求。
3.3.2 横向应力
普通螺栓横向应力校核的原则为在预紧力的作用下,横向力不能使被连接工件之间发生错动,根据机械设计手册传感器每个螺钉最大预紧力公式如下:
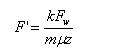 (4)
(4)
式中F"为每个螺钉受最大横向力;k为摩擦连接可靠性因子,取值范围为1.1~1.3,为了安全取1.3;m为结合面数,由于传感器与上夹具及螺钉垫片有2面结合,因此m=2;Fw为最大横向总受力25.38KN; 为结合面间摩擦因数,对于干燥的钢铁零件取值范围为0.1~0.16,为了安全取0.1;z为螺钉个数4。将k、Fw、m、 、z代入式(4)得F"=41.243KN。
仍然运用式(2),此处F0=F",将其余数值代入得 =356.7MPa<640/1.5=426.7MPa,横向应力符合安全要求。
3.3.3 螺钉扭矩计算及校核
螺钉扭矩与预紧力简化关系式如下:
![]() (5)
(5)
其中T为扭矩;F"为螺钉最大预紧力41.243KN;d为螺钉公称直径16mm,将F"、d代入式(5)得扭矩T=132Nm。因此在装配时只要每个M16螺钉安装扭矩不小于132Nm,就可以保证安全的预紧力。
对螺钉施加扭矩会使其产生剪切应力,因此必须对其进行校核,螺钉抗扭截面模量及校核扭转剪切应力计算式见式(6)、(7):
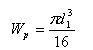 (6)
(6)
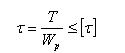 (7)
(7)
式中Wp为抗扭截面模量;d1为螺钉小径13.835mm; 为扭转剪切应力;T为扭矩132Nm; 为许用剪切应力,查表得在变载情况下, = /2.5=256MPa。将上述参数代入式(6)、(7)得 =254MPa< =256MPa,扭转剪切应力符合安全要求。