基于ANSYS方坯在加热炉升温过程中的热应力分析

　　1 前言

　　钢坯的再加热过程是为热轧生产进行金属组织准备的环节，在轧钢生产中占有十分重要的地位。钢坯的加热过程是影响设备运行和产品质量的重要因素：加热过程中，由于加热温度、内部热应力以及内部组织等的影响，常常会引起后部工序的缺陷，影响最终产品质量。但由于缺乏可行的检测手段，钢坯在加热过程中的温度分布及加热状况一直是依据经验和理论进行估算的。使得钢坯烧不透和过烧现象时有发生，也无法动态确定加热炉中钢坯的热炉质量[1，2]。

　　本工作是针对某厂步进式多段炉加热制度的优化进行的。在原加热制度下(工艺A加热时间为150min)，某钢种的钢坯经加热后部分出现断裂现象。针对这一问题，工作人员对加热制度进行了改进(加热时间150min延长为180min，加热温度降低)，改进后的加热制度解决了钢坯的断裂现象。本计算分别对改进前和改进后的工艺进行了温度场和应力场的计算，对工艺的优化在理论上给以解释。

　　2 计算用钢种的材料物性

　　计算用钢种的材料密度为：7840kg/m3;材料的导热系数及比热见表1。

　　表1.材料的导热系数及比热

　　3 几何模型及坐标

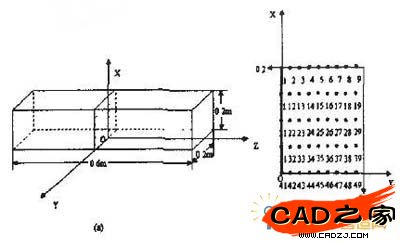
　　实际的钢坯端面为0.2m×0.2m 正方形，长度为10m。在实际计算，当长度方向为端面边长的3 倍以上时，端面对心部的热应力影响很小。所以在本计算中，建立了尺寸0.2m×0.2m×0.6m 的模型进行计算。计算温度场及应力场的几何模型见图1。

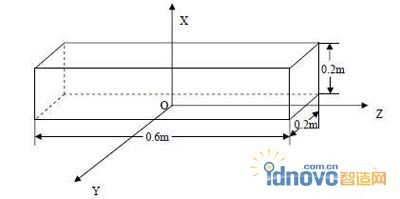
　　图1 几何模型及坐标

　　4 模型假设

　　由于加热炉的复杂性，在进行钢坯温度场和应力场计算时，需进行一些假定[3,4]：

　　(1)不考虑步进梁与钢坯之间的接触传热，认为钢坯周围全是炉气。

　　(2)钢坯与炉气的对流、辐射传热视为与无限大环境的传热。

　　(3)钢坯在加热炉各区段内是匀速运动的。

　　(4)钢的相变热通过比热的变化考虑进去。

　　5 计算结果及分析

　　针对两种不同的工艺，利用ANSYS 有限元平台，进行了温度-结构耦合计算。分别计算了不同加热段坯子的温度分布和应力强度分布[5]。

　　5.1 温度场分析

　　分别对两种不同工艺进行了温度场的计算，并根据模型的对称性，沿模型长度z 方向截取1/2 为分析对象。图2分别为两种工艺升温过程结束时温度场的分布，由图可看出钢坯表面温度高于心部，且角部温度最高。图3分别为两种工艺降温过程结束时温度场的分布，由图可看出钢坯心部温度高于表面，且角部温度最低，说明角部散热最快。

　　由于钢坯沿xy 平面断裂，所以截取z=0 处xy 面进行分析。由图2 可知，对于xy 面，在加热结束时心部温度最低，角部温度最高。由图3 可知，在加热结束时角部温度最低，心部温度最高。因此对两种工艺xy 面的心部和角部点的温度及温度差随时间变化进行比较(图4，其中(0.1，0，0)为心部点和(0，0.1，0)为角部点;图5)。

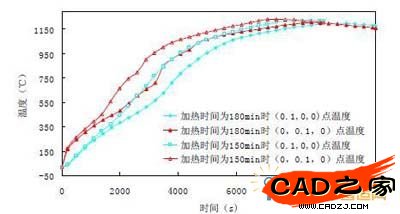
　　图 4 工艺A 和B，xy 面心部和角部点的温度-时间历程曲线

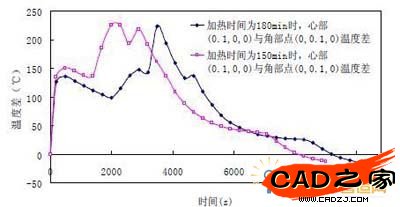
　　图 5 工艺A 和B，xy 面心部和角部点的温度差-时间历程曲线

　　由图 4 可以看出，加热制度修改前，在加热过程中，钢坯升温速度快。加热制度修改前，钢坯温度高于修改之后的钢坯温度。

　　由图5 可知对于工艺A(加热时间为150min)：在8200s 以前，角部温度高于心部温度，钢坯处于加热状态，在8200s 以后，角部温度低于心部温度，钢坯心部已经完成升温过程，并开始向表面传递热量。在2280s 时，温差达到最大(心部温度为520℃，角部为745℃，温差为225℃达到角部温度的30%)。

　　对于工艺B(加热时间为180min)：在9200s 以前，角部温度高于心部温度，钢坯处于加热状态，在9200s以后，角部温度低于心部温度，钢坯心部已经完成升温过程，并开始向表面传递热量。在3487s 时，温差达到最大(心部温度为629℃，角部为852℃，温差为223℃达到角部温度的26%)。

　　在加热初始阶段(300s 左右)，两种工艺的心部角部温度差很接近;在3200s 前，工艺A(加热时间为150min)心部角部温度差高于工艺B(加热时间为180min)。而在3200s 后，工艺A(加热时间为150min)心部角部温度差基本低于工艺B(加热时间为180min)。

　　5.2 应力强度分析

　　由于温度分布不均匀，将在钢坯内产生热应力。根据温度场的计算结果，对模型进行了热应力的计算。

　　由于钢坯沿 xy 面断裂，为确定断裂面在z 轴方向的位置，在本计算中，截取了位于钢坯中心的xz 面进行热应力分析(图6a)。图7 分别为两种工艺下，应力强度沿xz 面的分布云图，由图可看出，应力强度对称分布于z=0 平面两侧;中心部位应力强度较高，且随z 坐标的增大，应力强度降低;但是在接近表面时，应力强度增加。本计算只截取了z>0 的半个平面进行分析，我们沿分析面上的x 轴取五条线(x=0, 0.05, 0.1, 0.15, 0.2),并在这五条线上分别取10 个节点(图6b)进行应力强度分析。

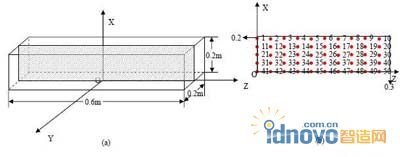
　　图6 热应力分析截取断面(a)及节点(b)

　　图7 应力强度沿xz 面的分布云图

　　图8 为x=0.2 线上节点的应力强度随时间变化的历程曲线，计算结果表明，在整个时间历程中，节点1(中心轴上节点)(见图6a)的应力强度最大，随z 坐标的增大，节点的应力强度逐渐降低，所以钢坯沿靠近中心xy面断裂。对于工艺A，节点应力强度在2280s 左右(预热段)出现最大值;对于工艺B，节点应力强度在3487s(加2 段)左右出现最大值。随后各点的应力强度随时间增加降低，且各点的应力强度逐渐趋于一致。这与温度场的结果相对应：对于工艺A，在2280s 左右(预热段)，钢坯温度差达到最大，对于工艺B，在3487s 左右(加2 段)，钢坯温度差达到最大。随后温度差随时间增加降低，各点的温度逐渐趋于一致，达到均热状态。

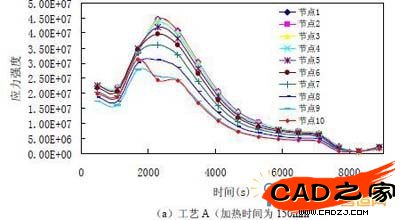
　　(a)工艺A(加热时间为150min

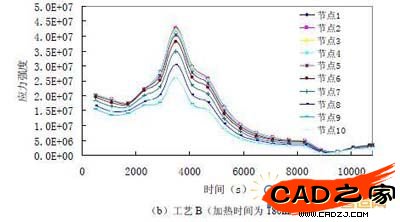
　　(b)工艺B(加热时间为180min)

　　图 8. 位于y=0 的xz 面上节点应力强度随时间变化的历程曲线

　　根据以上的分析结果，钢坯沿中心xy 面断裂，故我们截取位于z=0 的xy 面进行进一步的分析(图9a)。图10 分别为两种工艺下，应力强度沿xy 面的分布云图，由图可看出，应力强度对称分布于y=0 平面两侧;位于钢坯上表面角部应力强度最大，说明该处容易发生裂纹。本计算只截取了y>0 的半个平面进行分析，我们沿分析面上的x 轴取五条线(x=0, 0.05, 0.1, 0.15, 0.2),并在这五条线上分别取9 个节点(图9b)进行应力强度分析。

　　9热应力分析截面取断面(a)及节点(b)

　　图 10 应力强度沿XY 面的分布云图

　　图 11 为x=0.1 线上节点的应力强度随时间变化的历程曲线，计算结果表明，在整个时间历程中，节点21(中心轴上节点)(见图9a)的应力强度最大，随y 坐标的增大，节点的应力强度降低，在接近表面处，应力强度增加。对于工艺A，节点应力强度在2280s 左右(预热段)出现最大值;对于工艺B，节点应力强度在3487s(加2 段)左右出现最大值。随后各点的应力强度随时间增加降低，且各点的应力强度逐渐趋于一致。 根据前面的分析结果，对工艺A(加热时间为150min)在2280s 时位于xy 中间面x=0.2 上各节点的应力强度和工艺B(加热时间为180min)在3487s 时相应位置上各节点的应力强度进行比较(图12)。结果表明工艺经修改后，应力强度降低。并根据公式 计算了工艺修改后应力强度降低的百分数(图(13)。由图可知应力强度最大点(z=0 的xy面角部位置)降低了11.40%。

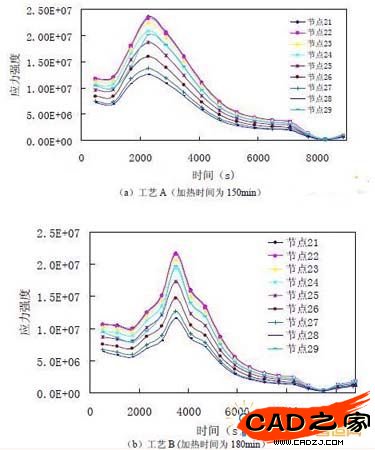
　　图 11.位于z=0 的xy 面上节点应力强度随时间变化的历程曲线

　　图 12. xy 中间面x=0.2 线上节点应力强度的比较

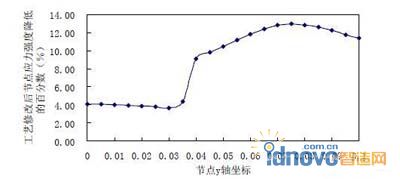
　　图 13.工艺修改后节点(位于xy 中间面x=0.2 线上)应力强度降低的百分数

　　6 结论

　　(1)工艺A 在2280s 左右(预热段)，钢坯温度差达到最大，节点应力强度在此时出现最大值;工艺B在3487s 左右(加2 段)，钢坯温度差达到最大，节点应力强度在此时出现最大值。

　　(2)从Y=0 的XZ 面上的应力强度分布可知：位于中心轴上的节点应力强度最大，随z 坐标的增大，节点的应力强度逐渐降低，所以钢坯沿靠近中心xy 面断裂。

　　(3)从z=0 的XY 面上的应力强度分布可知：应力强度对称分布于y=0 平面两侧;位于钢坯上表面角部应力强度最大，说明该处容易发生裂纹。

　　(4)计算结果表明：工艺经修改后，应力强度最大点(z=0 的xy 面角部位置)降低了11.40%。

　　(5)可适当加长预热段和加2 段时间，减少加1 段和均热段的时间，降低最大应力强度，使得应力强度在整个工艺过程均匀化，从而降低断裂的可能性。

　　(6)由于方坯的断裂原因很复杂，在理论分析上笔者还将要做进一步的工作。