基于MSC横向拉杆非线性屈曲优化

　　1 概述

　　机械结构的屈曲是工程实际中最关心的问题之一，屈曲失效也是工程中最常见的失效形式之一，在汽车结构中也是如此。因此，考察结构的屈曲也是汽车工程师的主要工作内容之一。横向拉杆的主要失效形式就是失稳，本文针对某轿车横向拉杆(如图1)进行非线性屈曲优化。

　　图1 横向拉杆

　　2 初始设计

　　2.1 初始设计模拟

　　初始设计为平板的厚度为5.8mm，材料的屈服极限为380MPa，立板的厚度为6.8mm，材料的屈服极限为480MPa，采用体单元进行网格划分,一端(节点101)采用固定铰约束，另一端采用滑移铰约束，在滑移铰约束端施加y方向40KN载荷，有限元模型如图2。用MSC Nastran非线性静态求解器riks弧长法求解。位移云图和位移-载荷曲线如图3，位移-载荷曲线的最高载荷点，即失稳点的载荷为28.5978kN。

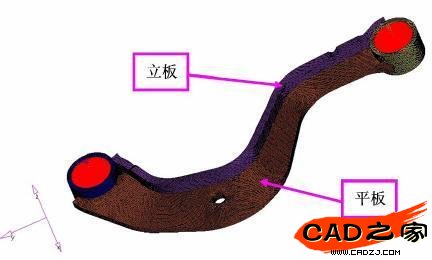
　　图2 横向拉杆的有限元模型

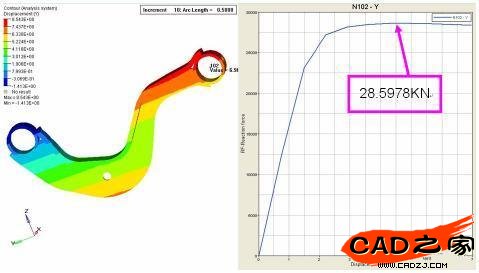
　　图3 位移云图和位移-载荷曲线

　　2.2初始设计静态加载试验

　　在实验台架上以10毫米/分钟的速度对试件进行静态加载直至试件发生屈服为止，试件的静态加载曲线如图4，试件静态加载试验和模拟结果对比如表1。模拟结果与实验数据非常吻合(误差仅为0.56%)，说明有限元模型可以模拟结构初始设计的真实工况而且模拟结果非常可靠，但是该结构不能满足工程实际要求(31KN)。因此，本文将从零件材料和零件厚度两个方面对该结构进行优化。

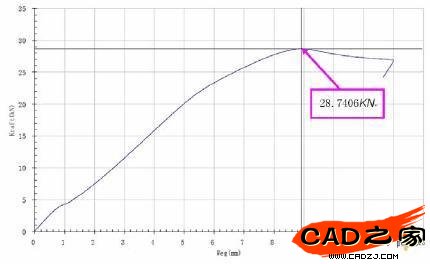
　　图4 试件静态加载曲线

　　表1 静态加载试验和模拟结果对比　

　　3 优化设计

　　根据该结构的结构特点和工况特点，以两个零件的厚度和两种材料的屈服极限作为设计变量、结构的屈服要大于等于31kN作为优化条件和结构的重量最轻作为优化目标对结构进行优化，即：

　　设计变量：

　　平板的厚度t1(mm):2.618.5≤≤t;

　　立板的厚度t2(mm): 0.728.6≤≤t;

　　平板的屈服极限y1(MPa): 4801380≤≤y;

　　立板的屈服极限y2(MPa): 5202480≤≤y;

　　设计条件：

　　屈服力≥31kN;

　　设计目标：

　　Minimize(Total_Weight(t1,t2,y1,y2))

　　部分优化结果如表2和表3。

　　表2 t1=5.8和t2=6.8时几种材料组合的模拟结果

　　表3 y1=460和y2=520时几种厚度组合的模拟结果　　

　　根据优化结果选用屈服极限为460MPa厚度为6.0的平板和屈服极限为520厚度为6.9的立板作为最终设计方案，该设计方案模拟结果屈服力为31.7981kN。对该设计方案进行静态加载试验验证，屈服力为31.9805kN,模拟结果的误差仅为0.57%，满足工程实际需要，并且该设计方案通过整车厂的验收。

　　4 结论

　　从表3的优化结果中可以看出提高平板的屈服极限比提高立板的屈服极限对结构的屈曲的提高更显著。

　　从表4的优化结果中可以看出增加平板的厚度比增加立板的厚度对结构的屈曲的提高更显著。

　　因此，平板的性能对整个结构屈曲的影响是主要的，提高平板的性能可以更有效的提高整个结构的屈曲稳定性。

　　采用仿真与试验相结合的手段，能够迅速解决设计开发中的问题，对于满足项目发放进度和提高企业竞争力是十分必要的。