在新型弧形钢闸门设计中拓扑优化的应用

　所谓结构拓扑优化是指结构中材料的布局优化，它能为形状/尺寸优化提供新颖、合理的初始设计。连续体结构拓扑优化理论始于20世纪80年代末，经过不断发展和完善，现已广泛应用于航空、航天、机械制造、复合材料设计等诸多领域。连续体拓扑优化方法中影响最大、应用最广的是变密度法(Solid Isotropic Microstructures with Penalization简称SIMP法)。目前，该方法已集成于多种结构分析软件，如HyperWorks、ANSYS等。

　　朱军祚等最早利用ANSYS中拓扑优化模块探讨了水工钢闸门的设计问题。该工作仅停留在理论探讨层面。为了使得拓扑优化能够有效地指导水工结构设计，尤其是弧形钢闸门的设计中。本文以一个现实的露顶式弧形钢闸门设计方案为例，采用分步拓扑优化方法进行了新型弧形钢闸门结构设计方法的探索。

　　1 连续体拓扑优化概念

　　1.1 SIMP方法的数学描述

　　在SIMP方法中，若结构分析材料有限元方法进行，则单元的伪密度为单元的设计变量，伪密度取值范围是(0 1]。伪密度趋于零表示单元中无材料，等于1则表示单元中材料无空隙。伪密度介于0和1之间的单元称为中间密度单元。为了便于提取边界，需减少中间密度单元的个数，因此往往采用密度惩罚的办法，即单元中材料的弹性模量与伪密度的p次方成正比。p即为密度惩罚因子，本文取其值为3。同时，为了避免棋盘格等数值不稳定现象的出现，需对目标函数的敏度做滤波处理。

　　通常，刚度优化设计问题可用下式表述：

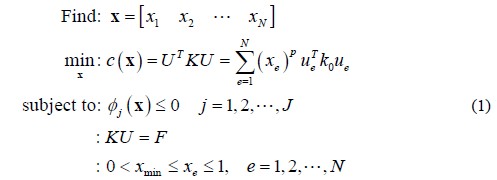
　　其中，U和F为全局位移向量和力向量，K为全局刚度矩阵，即结构总刚度阵，ue和ke是单元位移矢量和单元刚度矩阵，设计变量xe为单元的伪密度，xmin是伪密度下限(不为零，以避免结构总刚度阵奇异)，N为设计域内单元的个数，p是惩罚因子，φj为约束函数，如体积约束、位移约束、应力约束、屈曲约束和频率约束等。J为约束函数个数。1.2 结构拓扑优化的实现本文采用有限元软件HyperWorks的拓扑优化功能实现结构拓扑优化分析。

　　2 应用实例

　　2.1 工程概况

　　某水电站溢洪道工作弧门结构布置图如图1 a所示工作闸门结构设计为双腹板主横梁、斜支臂结构形式(支臂截面为箱型)，闸门结构各个部件布置情况见图2 所示。

　　(i) 闸门布置参数

　　孔口高度：20.0m

　　闸门高度：20.333m

　　底槛高程：455.167m

　　支铰高程：466.50m

　　弧门半径：24.00m

　　工作弧门20×20.333m2，设计水头19.833m，总水压力约39000KN。

　　(ii) 板件厚度

　　见附录1。

　　(iii) 材料参数

　　闸门所用材料为Q345B钢材，弹性模量为206GPa，泊松比为0.3，密度ρ=7800kg/m3。【结构总重约273吨】

　　图 1 工作弧门结构布置图

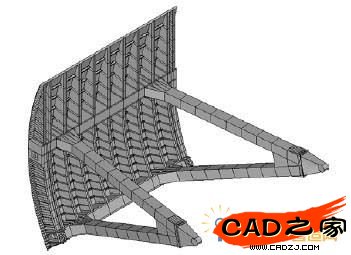
　　图 2 弧门结构的传统设计方案

　　2.2 设计步骤

　　大量的分析表明，如果采用三维实体结构直接进行拓扑优化，得到的结果往往难以制造，甚至无法为结构设计提供新思路。为此，本文采用逐步拓扑优化的方法将弧形钢闸门看作是由三个主要部件，即两个支臂、挡水面板和支撑挡水面板的框架，构成的三维结构。在设计该结构的过程中主要包括以下几个步骤：

　　1) 支臂的设计方案;

　　2) 支撑框架中纵向肋的布局;

　　3) 支撑框架中横向肋的布局;

　　4) 构造钢闸门的整体结构并安全性分析;

　　5) 其他工况下的结构安全性校核。

　　2.3 设计过程

　　为了便于计算及描述，全局坐标系设定为直角坐标系(OXYZ)：X向为从坐标原点沿水流方向指向上游为X轴正方向;从坐标原点竖直向上为Y轴正方向;过坐标原点、与过支铰中心线平行并指向右支铰的方向为Z轴正方向。

　　2.3.1 支臂的设计方案

　　支臂的确定包括支臂的位置、拓扑、形状和尺寸的确定。该闸门的原始设计形式采用的是露顶式直支臂弧形钢闸门，支臂截面形式为箱型，支臂与弧形挡水面正交。目前仍设定支臂所在平面与挡水面板所在曲面正交。

　　I: 主支臂的位置

　　两组支臂的位置可通过如图3 所示的外伸等直梁中支撑的位置确定。易知，在均布荷载作用下，为保证梁在支撑处的转角为零，利用材料力学中梁的变形分析可知支座距离中心的长度()占总长(#p#分页标题#e#

)的0.293。因此当弧形钢闸门的跨度为20000mm时，支臂中心应距离挡水面板纵对称面5860mm处。

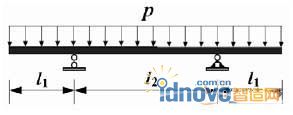
　　图 3 均布荷载作用下的外伸梁模型

　　II: 主支臂的拓扑、形状和尺寸

　　为了便于制造，在确定支臂拓扑、形状和尺寸时，现将原三维结构转化为二维分析，静水压力也相应地凝缩到二维边界。根据实际工程中钢闸门的侧视图，取二维的初始设计域为一个扇形(见图4 a)，扇形面的弧形半径即为工作弧门半径。

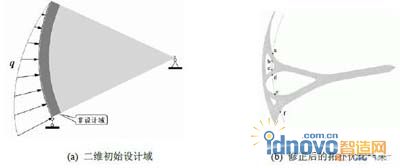
　　图 4 支臂拓扑优化模型及结果

　　在确定支臂拓扑时，工作弧门外表的挡水面板应设为非设计域。支臂与挡水面板之间应有纵向加强肋，以确保挡水面板受力均匀，变形小。此时，也设定加强肋所占区域为非设计域。因此，确定支臂拓扑、形状的二维初始设计中，非设计域的厚度由挡水面板的厚度和加强肋的厚度组成。该值需重新确定，其估算公式为：

　　其中：参数α取值范围为[10 20]，挡水面板的跨度L为200000mm，箱型支臂中纵向面内板的厚度D为4×30mm=120mm，挡水面板的厚度TO的初始值为16mm。同时，参考规范[1]，初步将二维初始设计中非设计区域深度取为1800mm。

　　扇形设计域中圆心位置及位移约束可按照图1中参数确定。挡水面板上的荷载q，即静水压力按满载(最不利工况)设定。图4 a所示的初始设计域中，材料选取Q345B钢材。拓扑优化的目标是结构柔度最小，约束条件为优化后的结构体积(即材料用量)占总体积的14%(即临界体积率为14%)。本次优化过程中暂不考虑结构自重，否则自重占据荷载主体，最终结构不利于抵挡水压力。图4 b为优化后并经修正得到的支臂形状(具体尺寸可参见附录2)。

　　2.3.2 纵向肋的布局方案

　　纵向肋是构成挡水面板的支撑框架的一部分。其布局方案包括，结构中纵向肋的数量、位置以及不同位置处纵向肋的深度。

　　为了获得纵向肋的布局方案，取三维结构中任意一个横截面(与图4 a中结构正交)，其模型如图3 中外伸梁，但梁的深度为2000mm，即略高于纵向肋最大深度(1800mm)，以便消除自由度约束处局部刚度过大现象;宽度为10000mm，即整体结构的一半。梁下位移约束设定为1100mm，即支臂的宽度，荷载为均布压力。其结构分析模型的一半为图5 a所示。在优化过程中，仅将挡水面板设定为非设计域，结构柔度最小为优化目标，具有体积约束(临界体积率为20%)。对其进行拓扑优化，优化后得到弧形挡水面中纵向肋数量、位置及深度(如图5 b所示)。

　　同时参照规范对部分尺寸进行了修正，得到结构初始设计的具体尺寸，如表1所示。所有纵向肋均采用工字钢。由此可以建立纵向肋的布局方案(参见图5 c)。

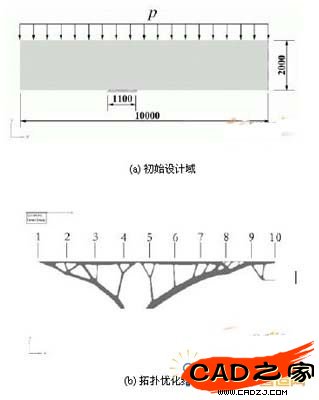
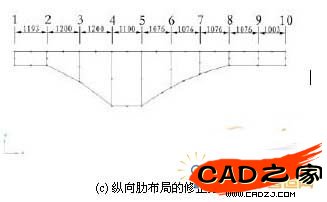
　　图 5 纵向肋布局优化及结果

　　表 1 纵向肋的深度

　　2.3.3 横向肋的布局方案

　　横向肋包括结构中部肋和边界肋。边界肋即为挡水面板上下两条边界上布设的肋。而中部布设的肋需通过拓扑优化分析获得。

　　图 6 为横向肋拓扑优化的初始设计域示意图。为了降低计算量，将支臂所在非设计区域去掉，交界处代之以固定位移约束。图6 b和6 c为横向肋拓扑优化的初始设计域三维视图。

　　对整体三维结构(见图6 c)进行拓扑优化，在优化过程中，仅将挡水面板设定为非设计域，结构柔度最小为优化目标，具有体积约束(临界体积率为10%)，并沿Z向施加生产制造(碾压成型)约束。

　　图 6 横向肋布局优化初始设计

　　拓扑优化后得到弧形挡水面的支撑框架中横向肋位置的初始设计方案，如图7 所示。图7 b中1号线上侧有材料，但没有布置肋。

　　修正后各个1-8号横向肋与0号线夹角的角度(参见表2)。因横向肋与纵向肋相互卡接，纵向肋的间距小，所以横向肋均采用矩形截面钢(平面钢板)。由此建立横向肋的布局方案(参见图7 b)。

　　 #p#分页标题#e#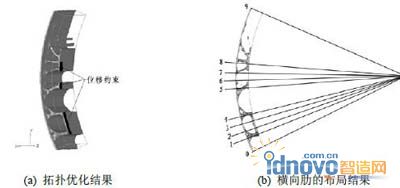

　　图 7 横向肋布局优化及结果

　　表 2 横向肋的布置角度

　　此外，除了上述横向肋外，挡水面板的上下边界也需布设横向肋。这两根横向肋(0号和9号)无卡槽，不仅能提高结构刚度、加强纵向肋的稳定性，同时也有利于提高结构强度。尤其是底部横向肋(0号)上与支臂交叉处将布设吊耳。因此，挡水面板的支撑框架内含有10根横向肋。

　　2.3.4 建立结构初始设计模型并做安全性分析

　　根据以上分步拓扑优化结果，可以得到模型的支臂、纵向肋和横向肋等部分的布局方案。挡水面板的支持框架中含19根纵向肋(10号纵向肋处在钢闸门的对称面内)。利用各部件的设计方案建立弧形钢闸门的三维模型(参见图8 )。各部件初始尺寸可参见附录1。

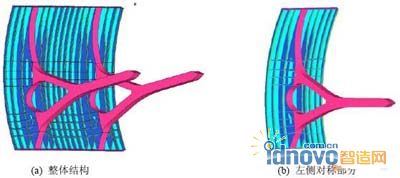
　　图 8 弧形钢闸门整体结构初始设计

　　满载工况是指结构考虑自重的情况下，工作水头达到设计水头(19.833m)时结构的受力状态。非满载时，结构中除自重外，还可能存在不同水头下的静水压力荷载。

　　分析过程中，因支铰处没有设计支撑细节，因此支铰及附近1.8m范围内的应力将不作为参考。

　　(i)刚度校核

　　满载条件下结构分析得到位移云图(见图9)。可发现，弧形挡水面的上部位移相对较大，而实际中弧形挡水面上部受到的荷载作用是相对较小的。位移最大值为65.2mm，位于挡水面上部的两个角端位置;两侧纵向肋中部和底部位移较小且比较均匀，介于10~20mm之间，底部最低点的位移为14.7mm;面板中部偏下和底部位移较大，介于25~37mm之间。

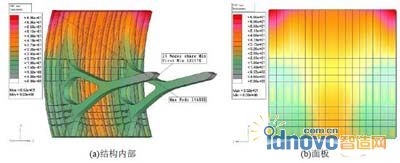
　　图 9 结构位移云图

　　(ii)强度校核

　　满载条件下结构的应力云图如图10所示。从图中可以看出，应力高于345MPa的区域是支铰附近区域范围内，原因在于在分析时仅作线弹性分析。但该部分需做圆柱铰，细节改变后受力状态也会改变。支臂中除支撑点外的最大应力出现在上部主干直支臂与分支臂过渡区(如图10中A点)，最大应力值为260MPa，支臂的其余部分应力均小于210MPa;纵向肋中应力最大的位置是支臂连接的外侧纵向肋(4号纵向肋)的下部，与面板和横向肋连接的局部范围内(如图10中B点)其值为494MPa(大于345MPa)，需要做局部加强处理。除了与横向肋连接处应力相对较大外，纵向肋的其余部分应力值均小于170MPa;横向肋中应力最大的位置是2号横向肋与支臂内侧连接处(如图10中C点)，其值为332.6MPa，除了与支臂连接处应力相对较大外，横向肋的其余部分应力值均小于175MPa;挡水面板中应力最大的位置是4号纵向肋与面板的下部连接处，其值为308.8MPa，挡水面板中除最下层面板外，面板的其余部分应力值均小于205MPa。

　　图 10 结构应力云图

　　(iii)屈曲稳定性校核

　　对所建立的模型施加实际的约束和荷载之后，进行模态分析。一阶模态如图11所示，首先进入失稳的位置在上部支臂与7号横向肋交界附近，对应的屈曲临界荷载因子为3.514(远大于1.0)。因重力为不变荷载，因此真实值大于3.514。

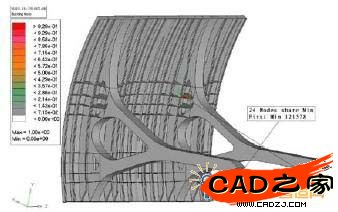
　　图 11 闸门的一阶模态

　　(iv)动力稳定性校核

　　通常，水流激励频率在[0 3]之间。为了避免结构发生共振，需避开此区间。对上述结构进行自振分析。一阶频率(基频)为4.266，远离水流频率。因此结构满足动力稳定性。2.3.5其他工况下的结构安全性校核(i)非满载工况表3给出了不同工况下结构中应力和位移最大值及所处位置。不难发现，满载时底部四号纵向肋应力超过许用应力，需做局部加强。

　　表3 不同水头下结构中最大应力及最大位移

　　(ii)满载下吊耳工作工况

　　吊耳工作时可看作是将吊耳所在位置上的节点沿Y向指定一个很小的位移值。底部横向肋上其他点的位移约束全部去掉。结构的最大位移值为66.5mm，位于面板上部中间;结构中除支铰外的其他部分受力比较均匀，应力值均小于259MPa。

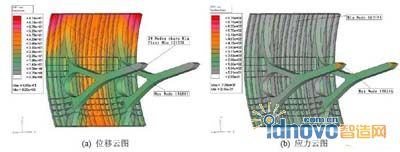
　　图 12 吊耳工作时满载结构位移及应力分布#p#分页标题#e#

　　3 结论

　　利用优化方法并结合实例设计了新型弧形闸门，给出了设计露顶式弧形钢闸门的设计步骤。在确保结构的强度、刚度和稳定性等性能指标具有一定安全裕度条件下，经优化后结构重量较传统设计减重约26%。结构自重大大降低的优点在于：节省材料、降低造价、便于安装和操作。